K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
mình đang cần gấp 
2
7 tháng 5 2017
\(x-y=9\Rightarrow x=9+y\Rightarrow y=x-9\)
Ta có:
\(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)
\(=\dfrac{3x+x-9}{3x+y}-\dfrac{3y+y+9}{3y+x}\)
\(=\dfrac{3x+\left(x-9\right)}{3x+y}-\dfrac{3y+\left(y+9\right)}{3y+x}\)
\(=\dfrac{3x+y}{3x+y}-\dfrac{3y+x}{3y+x}\)
\(=1-1\)
\(=0\)
Vậy biểu thức \(\dfrac{4x-9}{3x+y}-\dfrac{4y+9}{3y+x}\)khi \(x-y=9\) là 0
5 tháng 5 2017
\(x-y=9\Rightarrow y=x-9\) thay vào biểu thức B ta được :
\(B=\dfrac{4x-9}{3x+\left(x-9\right)}-\dfrac{4\left(x-9\right)+9}{3\left(x-9\right)+x}=\dfrac{4x-9}{4x-9}-\dfrac{4x-27}{4x-27}=1-1=0\)
Vậy giá trị của B là 0 tại \(x-y=9\)
24 tháng 10 2017
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
24 tháng 10 2017
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)
DT
Đỗ Thanh Hải
CTVVIP
5 tháng 11 2017
Với mọi x ta có:
|x - 2001| = |2001 - x|
=> A = |x - 2002| + |2001 - x|
Với mọi x ta cũng có:
|x - 2002| + | 2001 - x| \(\ge\)|(x - 2002) + (2001 - x)|
A \(\ge\) |1|
A \(\ge\) 1
Dấu bằng xảy ra <=> (x - 2002).(2001 - x) \(\ge\) 0
=> x - 2002 \(\ge\) 0; 2001 - x \(\ge\) 0 (1)
hoặc x - 2002 \(\le\) 0; 2001 - x \(\le\) 0 (2)
Từ (1) => x > hoặc = 2002; x < hoặc = 2001 => x không có giá trị thoả mãn
Từ (2) => x < hoặc = 2002 ; x > hoặc = 2001 => 2001 \(\le\) x \(\le\) 2002
Vậy 2001 \(\le\) x \(\le\) 2002 thì A có giá trị nhỏ nhất = 1
25 tháng 10 2017
b) Vì 50 > 49 nên \(\sqrt{50}\) > \(\sqrt{49}\) = 7
Vì 2 > 1 nên \(\sqrt{2}\) > \(\sqrt{1}\) = 1
\(\Rightarrow\) \(\sqrt{50}\) + \(\sqrt{2}\) > 7 + 1 = 8 (1)
Ta nhận thấy: 50 + 2 = 52 < 64. \(\Rightarrow\) \(\sqrt{50+2}\) < \(\sqrt{64}\) = 8 (2)
Từ (1) và (2) suy ra \(\sqrt{50}\) + \(\sqrt{2}\) > \(\sqrt{50+2}\)
Vậy,...
25 tháng 10 2017
OK, tôi sẽ giúp bn.
a) Vì 26 > 25 nên \(\sqrt{26}\) > \(\sqrt{25}\) = 5
Vì 17 > 16 nên \(\sqrt{17}\) > \(\sqrt{16}\) = 4
\(\Rightarrow\) \(\sqrt{26}\) + \(\sqrt{17}\) > 5 + 4 = 9
Vậy, \(\sqrt{26}\) + \(\sqrt{17}\) > 9
HD
Hà Đức Thọ
Admin
11 tháng 3 2017
Em vào đây nhé Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
12 tháng 3 2017
Vẽ hình trực tuyến trên hoc24 | Hướng dẫn tạo khóa học trên hoc24 | Học trực tuyến
Ấn vào cái chữ màu xanh nhé!
Cậu nào giải được giải giúp tớ với
TT
7 tháng 10 2017
\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
7 tháng 10 2017
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)
1 tháng 6 2022
\(\dfrac{a+5}{a-5}=\dfrac{b+6}{b-6}\)
\(\Leftrightarrow\left(a+5\right)\left(b-6\right)=\left(a-5\right)\left(b+6\right)\)
\(\Leftrightarrow ab-6a+5b-30=ab+6a-5b-30\)
=>-6a+5b=6a-5b
=>-12a=-10b
=>6a=5b
hay a/b=5/6
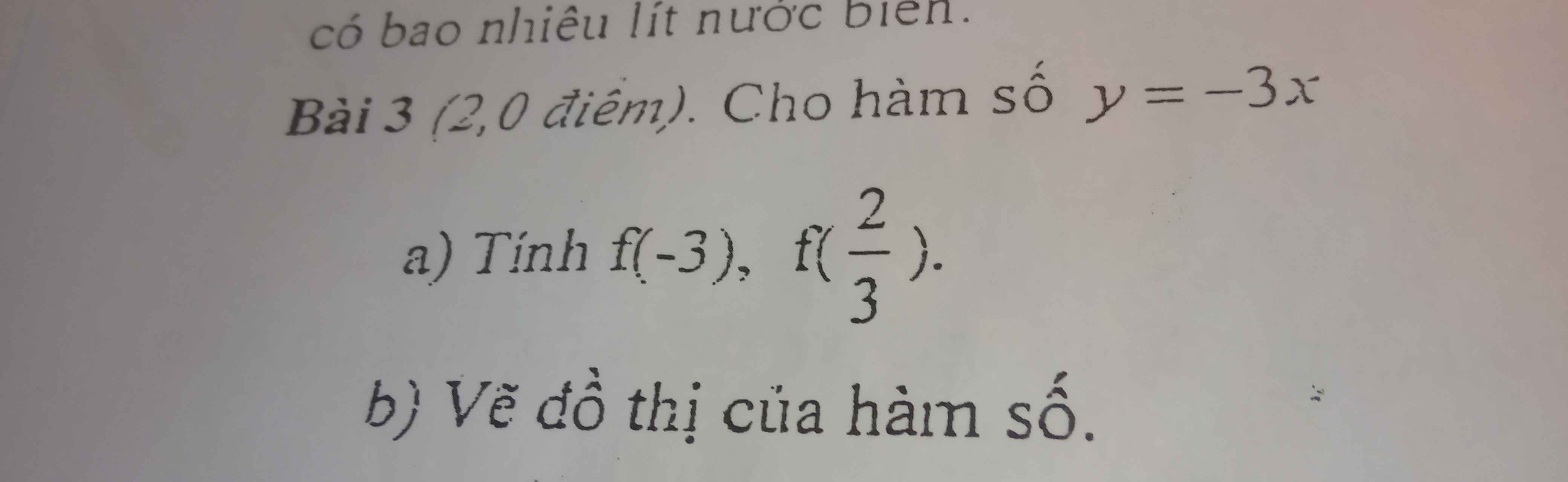
a: f(-3)=9
f(2/3)=-2