NP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
2
28 tháng 8
a:
b: TH1: \(\hat{BAD}>90^0;\hat{ABD}>90^0\)
Ta có: ABCD là hình thang
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{BCD}<180^0-90^0=90^0\)
=>\(\hat{BCD}<\hat{BAD}\)
TH2: \(\hat{ADC}>90^0;\hat{DCB}>90^0\)
Ta có: ABCD là hình thang
DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(\hat{DAB}<180^0-90^0=90^0\)
=>\(\hat{DAB}<\hat{DCB}\)
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
P
1
28 tháng 8
a:
b: TH1: \(\hat{BAD}>90^0;\hat{ABD}>90^0\)
Ta có: ABCD là hình thang
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{BCD}<180^0-90^0=90^0\)
=>\(\hat{BCD}<\hat{BAD}\)
TH2: \(\hat{ADC}>90^0;\hat{DCB}>90^0\)
Ta có: ABCD là hình thang
DC//AB
=>\(\hat{CDA}+\hat{DAB}=180^0\)
=>\(\hat{DAB}<180^0-90^0=90^0\)
=>\(\hat{DAB}<\hat{DCB}\)
c: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó: ABCD là hình bình hành
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
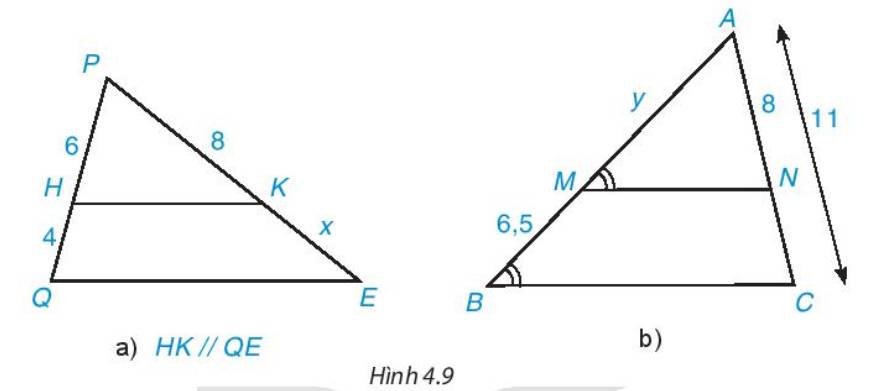
• Hình 4.9a)
Vì HK // QE nên áp dụng định lí Thalès, ta có:
\(\dfrac{{PH}}{{QH}} = \dfrac{{PK}}{{KE}}\)hay \(\dfrac{6}{4} = \dfrac{8}{x}\)
Suy ra \(x = \dfrac{{8.4}}{6} = \dfrac{{16}}{3} \approx 5,3\) (đvđd).
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
• Hình 4.9b)
Vì \(\widehat {AMN} = \widehat {ABC};\widehat {AMN}\) và \(\widehat {ABC}\) là hai góc đồng vị nên MN // BC.
Ta có AB = AM + BM = y + 6,5.
Áp dụng định lí Thalès, ta có: \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}}\) hay \(\dfrac{y}{{y + 6,5}} = \dfrac{8}{{11}}\)
Suy ra 11y = 8(y + 6,5)
11y = 8y + 52
11y – 8y = 52
3y = 52
\(y = \dfrac{{52}}{3} \approx 17,3\) (đvđd)
Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).
11 tháng 8
1: \(\frac{1-a\cdot\sqrt{a}}{1-\sqrt{a}}=\frac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)^{}}{1-\sqrt{a}}=1+\sqrt{a}+a\)
2: \(\frac{\sqrt{x+3}+\sqrt{x-3}}{\sqrt{x+3}-\sqrt{x-3}}=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}{\left(\sqrt{x+3}-\sqrt{x-3}\right)\left(\sqrt{x+3}+\sqrt{x-3}\right)}\)
\(=\frac{\left(\sqrt{x+3}+\sqrt{x-3}\right)^2}{x+3-\left(x-3\right)}=\frac{x+3+x-3+2\sqrt{\left(x+3\right)\left(x-3\right)}}{6}\)
\(=\frac{2x+2\sqrt{x^2-9}}{6}=\frac{x+\sqrt{x^2-9}}{3}\)
4: \(\frac{3}{2\sqrt{9x}}=\frac{3}{2\cdot3\sqrt{x}}=\frac{1}{2\sqrt{x}}=\frac{\sqrt{x}}{2}\)
5: \(\frac{1}{2\sqrt{x}}=\frac{1\cdot\sqrt{x}}{2\sqrt{x}\cdot\sqrt{x}}=\frac{\sqrt{x}}{2x}\)
7: \(\frac{\sqrt{a^3}+a}{\sqrt{a}-1}=\frac{a\cdot\sqrt{a}+a}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)}{\sqrt{a}-1}=\frac{a\left(\sqrt{a}+1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\frac{a\left(a+2\sqrt{a}+1\right)}{a-1}=\frac{a^2+2a\cdot\sqrt{a}+a}{a-1}\)
8: \(\frac{2}{\sqrt{a}+\sqrt{2b}}=\frac{2\cdot\left(\sqrt{a}-\sqrt{2b}\right)}{\left(\sqrt{a}+\sqrt{2b}\right)\left(\sqrt{a}-\sqrt{2b}\right)}=\frac{2\sqrt{a}-2\sqrt{2b}}{a-2b}\)
10: \(\frac{25}{\sqrt{a}-\sqrt{b}}=\frac{25\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{25\sqrt{a}+25\sqrt{b}}{a-b}\)
11: \(-\frac{ab}{\sqrt{a}-\sqrt{b}}=-\frac{ab\left(\sqrt{a}+\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}=\frac{-ab\cdot\sqrt{a}-ab\cdot\sqrt{b}}{a-b}\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 1 2024
Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)
HQ
1
HQ
Hà Quang Minh
Giáo viên
12 tháng 1 2024
\({x^6} + {y^6} = {\left( {{x^2}} \right)^3} + {\left( {{y^2}} \right)^3} = \left( {{x^2} + {y^2}} \right)\left[ {{{\left( {{x^2}} \right)}^2} - {x^2}.{y^2} + {{\left( {{y^2}} \right)}^2}} \right] = \left( {{x^2} + {y^2}} \right)\left( {{x^4} - {x^2}{y^2} + {y^4}} \right)\)
15 tháng 8
a: Xét ΔKAD và ΔBDA có
\(\hat{KAD}=\hat{BDA}\) (hai góc so le trong, AK//BD)
AD chung
\(\hat{KDA}=\hat{BAD}\) (hai góc so le trong, AB//CD)
Do đó: ΔKAD=ΔBDA
=>KA=BD
mà BD=AC
nên AK=AC
=>ΔAKC cân tại A
b: ΔAKC cân tại A
=>\(\hat{AKC}=\hat{ACK}\)
mà \(\hat{AKC}=\hat{BDC}\) (hai góc đồng vị, BD//AK)
nên \(\hat{BDC}=\hat{ACD}\)
Xét ΔBDC va ΔACD có
BD=AC
\(\hat{BDC}=\hat{ACD}\)
CD chung
Do đó: ΔBDC=ΔACD
=>\(\hat{BCD}=\hat{ADC}\)
=>ABCD là hình thang cân
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
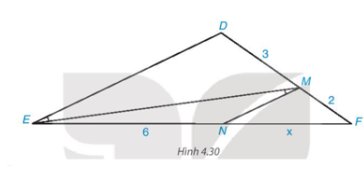
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).
BM
1
17 tháng 8
Bài 2:
a: \(\left(-\frac13x^2y\right)\cdot2xy^3=\left(-\frac13\cdot2\right)\cdot x^2\cdot x\cdot y\cdot y^3=-\frac23x^3y^4\)
b: \(\left(-\frac34x^2y\right)\cdot\left(-xy\right)^3=\left(-\frac34\right)\cdot\left(-1\right)\cdot x^2\cdot x^3\cdot y\cdot y^3=\frac34x^5y^4\)
c: \(\frac35\cdot x^2y^5\cdot x^3y^2\cdot\frac{-2}{3}=\left(\frac35\cdot\frac{-2}{3}\right)\cdot x^2\cdot x^3\cdot y^5\cdot y^2=-\frac25x^5y^7\)
d: \(\left(\frac34x^2y^3\right)\cdot\left(2\frac25x^4\right)=\frac34x^2y^3\cdot\frac{12}{5}x^4=\frac34\cdot\frac{12}{5}\cdot x^2\cdot x^4\cdot y^3=\frac95x^6y^3\)
e: \(\left(\frac{12}{15}x^4y^5\right)\cdot\left(\frac59x^2y\right)=\frac45\cdot\frac59\cdot x^4\cdot x^2\cdot y^5\cdot y=\frac49x^6y^6\)
f: \(\left(-\frac17x^2y\right)\left(-\frac{14}{5}x^4y^5\right)=\frac17\cdot\frac{14}{5}\cdot x^2\cdot x^4\cdot y\cdot y^5=\frac25x^6y^6\)
Bài 1: Các đơn thức là \(x^2y;-13;\left(-2\right)^3xy^7\)
a: =>x(x-3)(x+3)=0
=>\(x\in\left\{0;3;-3\right\}\)
b:=>(x-2)(x-2-x-5)=0
=>x-2=0
=>x=2
c:=>(x-3)^2=0
=>x-3=0
=>x=3
d: =>(x-1)(x-6)=0
=>x=1 hoặc x=6