Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3

a, \((\dfrac{-1}{2})\)2 -\(\dfrac{5}{6}\).\((\dfrac{-6}{7})-\dfrac{3}{4}:1\dfrac{2}{3}\)
=\(\dfrac{1}{4}+\dfrac{5}{7}-\dfrac{9}{20}\)
=\(\dfrac{35}{140}+\dfrac{100}{140}-\dfrac{63}{140}\)
=\(\dfrac{72}{140}\)= \(\dfrac{18}{35}\)

Ta có :
\(\left(3n+2\right)^4=\left(3n+2\right)^6\)
\(\Leftrightarrow\left(3n+2\right)^6-\left(3n+2\right)^4=0\)
\(\Leftrightarrow\left[\left(3n+2\right)^2-1\right]-\left(3n+4\right)^4=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[\left(3n+2\right)^2-1\right]=0\\\left(3n+2\right)^4=0\end{matrix}\right.\)
+)\(\left(3n+2\right)^4=0\)
\(\Leftrightarrow n=\dfrac{2}{3}\)\(\left(tm\right)\)
+) \(\left[\left(3n+2\right)^2-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}3n+2=1\\3n+2=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=\dfrac{-1}{3}\\n=-1\end{matrix}\right.\)\(\left(tm\right)\)
Vậy ....................


\(\left(4x-3\right)\left(\dfrac{3}{5}x+\dfrac{1}{2}\right)=0\)
\(=>4x-3=0\) hoặc \(\dfrac{3}{5}x+\dfrac{1}{2}=0\)
\(=>x=\dfrac{3}{4}\) hoặc x = -5/6
(4x - 3).(\(\dfrac{3}{5}\)x + \(\dfrac{1}{2}\)) = 0
=> TH1: 4x - 3 = 0
=> 4x =3
=> x = loại
=>TH2: (\(\dfrac{3}{5}\)x + \(\dfrac{1}{2}\)) = 0
=> \(\dfrac{3}{5}\) x = \(\dfrac{1}{2}\)
=> x = \(\dfrac{1}{2}\): \(\dfrac{3}{5}\)
=> x = \(\dfrac{5}{6}\)

gọi d là UCLN ( 2n+1;2n\(^2\)+2n)
2n+1\(⋮\)d=> n(2n+1)\(⋮\)d=> (2\(n^2\)+n)\(⋮\)d
2n\(^2\)+nchia hết cho d
=> ( 2n\(^2\)+2n-(\(2n^2\)+n))\(⋮\)d
mà n\(⋮d\)
2n+1chia hết cho d
=> 2n+1-2n chia hết cho d
<=> 1chia hết cho d => d =1
vậy 2n+1.2n(n+1) luôn tối giản với \(\forall\) n


Đo thanh gỗ có chiều dài \(:L\)
Nối sợi dây tới điểm có độ dài : \(\dfrac{L}{2}\)
=> Ta chia được thanh gỗ thành 2 phần bắng nhau
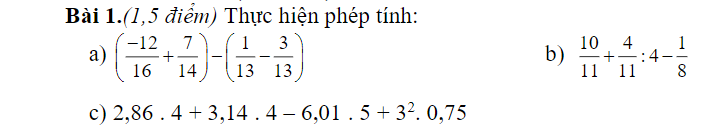

 c
c
 uc
uc cac ban oi giup mik voi mai minh hoc roi
cac ban oi giup mik voi mai minh hoc roi
giup minh voi may ban oi
a: =-3/4+1/2-1/13+3/13=-1/4+2/13=-13/52+8/52=-5/52
b: =10/11+1/11-1/8=1-1/8=7/8
c: =4(2,86+3,14)-30,05+9x0,75
=24-30,05+6,75
=0,7