
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Vẽ đồ thị độ dịch chuyển – thời gian: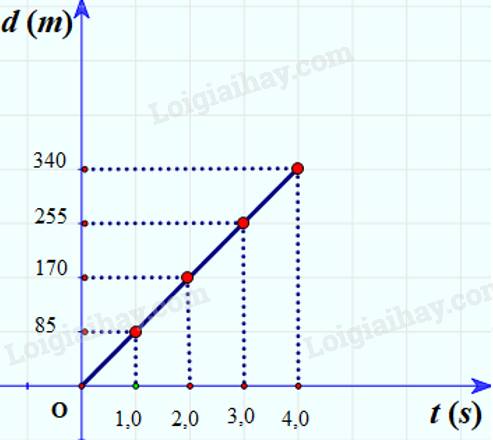
- Vận tốc của xe là:
\(v=\dfrac{d}{t}=85\left(m/s\right)\)

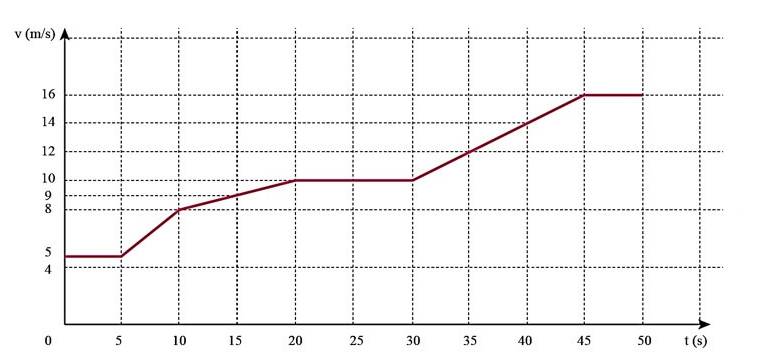
Mô tả chuyển động của vận động viên:
+ Từ 0 – 5 s đầu, vận động viên chuyển động thẳng đều
+ Từ 5 – 20 s tiếp theo, vận động viên chuyển động nhanh dần
+ Từ 20 – 30 s, vận động viên chuyển động thẳng đều
+ Từ 30 – 45 s, vận động viên chuyển động nhanh dần
+ Từ 45 – 50 s, vận động viên chuyển động thẳng đều.

1.
a) Vẽ đồ thị độ dịch chuyển – thời gian:
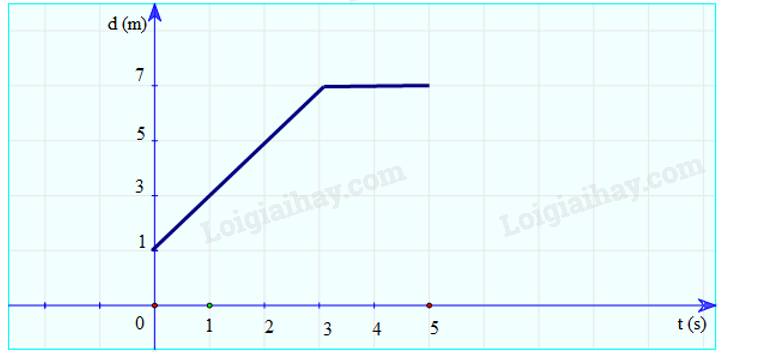
b) Mô tả chuyển động của xe:
- Từ 0 – 3 giây: xe chuyển động thẳng.
- Từ giây thứ 3 đến giây thứ 5: xe đứng yên (dừng lại)
c) Độ dịch chuyển của xe trong 3 giây đầu là:
\(d = 7 - 1 = 6m\)
Vận tốc của xe trong 3 giây đầu là:
\(v = \frac{{\Delta d}}{{\Delta t}} = \frac{6}{3} = 2\left( {m/s} \right)\)
2.
a) Mô tả chuyển động của xe:
- Trong 2 giây đầu: xe chuyển động thẳng
- Từ giây thứ 2 đến giây thứ 4: xe đứng yên
- Từ giây thứ 4 đến giây thứ 10: xe chuyển động thẳng theo chiều ngược lại.
- Từ giây thứ 9 đến giây thứ 10: xe dừng lại.
b)
- Ở giây thứ 2: xe ở vị trí cách điểm xuất phát 4 m.
- Ở giây thứ 4: xe ở vị trí cách điểm xuất phát 4 m
- Ở giây thứ 8: xe trở về vị trí xuất phát
- Ở giây thứ 10: xe ở vị trí cách điểm xuất phát 1 m theo chiều âm
c) Xác định tốc độ và vận tốc của xe:
- Trong 2 giây đầu, xe chuyển động thẳng, không đổi chiều nên tốc độ bằng vận tốc:
\(v = \frac{d}{t} = \frac{4}{2} = 2\left( {m/s} \right)\)
- Từ giây 2 đến giây 4: xe đứng yên nên vận tốc và tốc độ của xe đều bằng 0.
- Từ giây 4 đến giây 8:
+ Tốc độ: \(v = \frac{s}{t} = \frac{4}{4} = 1\left( {m/s} \right)\)
+ Vận tốc: \(v = \frac{{\Delta d}}{{\Delta t}} = \frac{{0 - 4}}{{8 - 4}} = - 1\left( {m/s} \right)\)
d)
- Từ đồ thị, ta thấy quãng đường đi được của xe sau 10 giây chuyển động là:
\(s = 4 + 4 + 1 = 9\left( m \right)\)
- Độ dịch chuyển của xe sau 10 giây là:
\(d = - 1 - 4 + 4 = - 1\left( m \right)\)
=> Quãng đường và độ dịch chuyển của xe sau 10 giây không giống nhau vì xe chuyển động theo 2 chiều.

a)
- a phụ thuộc vào F (m + M = 0, 5kg)
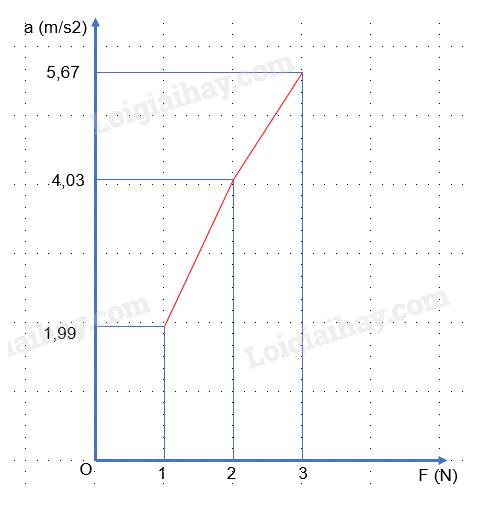
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
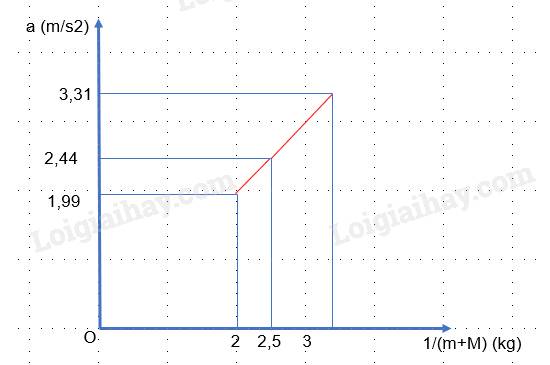
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

a) Vẽ đồ thị:
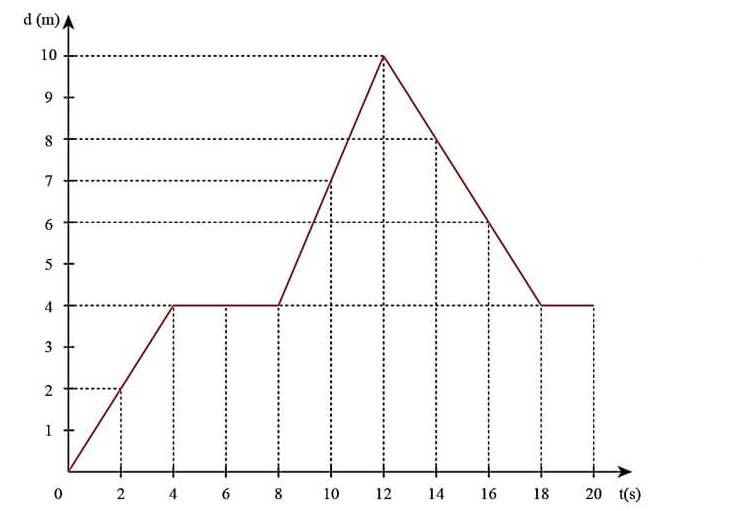
b)
- Vận tốc tức thời:
+ t = 2 s: \(v = \frac{d}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{d}{t} = \frac{4}{4} = 1(m/s)\)
+ t = 6 s: \(v = \frac{d}{t} = \frac{4}{6} \approx 0,67(m/s)\)
+ t = 10 s: \(v = \frac{d}{t} = \frac{7}{{10}} = 0,7(m/s)\)
+ t = 16 s: \(v = \frac{d}{t} = \frac{6}{{16}} = 0,375(m/s)\)
- Tốc độ tức thời:
+ t = 2 s: \(v = \frac{s}{t} = \frac{2}{2} = 1(m/s)\)
+ t = 4 s: \(v = \frac{s}{t} = \frac{{2 + 4}}{4} = 1,5(m/s)\)
+ t = 6 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4}}{6} \approx 1,67(m/s)\)
+ t = 10 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7}}{{10}} = 2,1(m/s)\)
+ t = 16 s: \(v = \frac{s}{t} = \frac{{2 + 4 + 4 + 4 + 7 + 10 + 8 + 6}}{{16}} = 2,8125(m/s)\)