Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

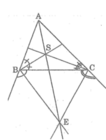
Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)
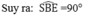
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)

Xét tứ giác BSCE ta có:
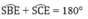
Vậy tứ giác BSCE nội tiếp đường tròn

A B C D I M E x y
a) Trong tam giác ABC cóE là giao điểm 2 phân giác trong góc B và C nên AE là phân giác góc BAC
Khi đó AE và AD đều là phân giác trong của góc BAC
=> 3 điểm A,E,D thẳng hàng
b) Có: ACB+BCx =180
=> 1/2 ACB +1/2 BCx =90
=> DCB + BCE =90
=> DCE =90
Tương tự : DBE =90
Trong tứ giác BECD CÓ DBE +DCE =90+90=180
=> TỨ giác BECD nội tiếp
c) theo câu b thì tứ giác BECD nội tiếp nên
DCB =DEB ( 2 góc nội tiêp cung chắn cung BD)
Xét tam giác DIC và tam giác BIE có :
DCB=DEB (cmt)
DIC= BIE ( 2 góc đối đỉnh)
=> tam giác DIC đồng dạng với tam giác BIE
=>\(\frac{BI}{ID}\)=\(\frac{IE}{IC}\)
=> BI *IC= ID*IE
mình ghi lại câu a nhé
Vì E là giao điểm của 2 đường phân giác trong của góc B,C nên E cũng thuộc đường phân giac của góc A
=> AE là phân giác góc A
Vì D là giao điểm của 2 đường phân giác các góc ngoài của góc B,C nên ta có D cách đều 2 cạnh AB,AC
=> D thuộc đường phân giác góc A
=>AE,AD nhau
=> A,E,D thẳng hàng

Tự Vẽ Hình Nhé :
Theo tính chất đường phân giác ngoài của một góc luôn vuông góc với đường phân giác ngoài của góc đó
=> \(\widehat{MBN}=\widehat{MCN}=90^0\)nên hai góc \(\widehat{MBN}\)và \(\widehat{MCN}\)cùng nhìn MN dưới một góc bằng 90 độ. vậy Tứ giác MBNC nội tiếp đường tròn đường kính MN
mk ko có bít làm sao jờ ?
?????????????????
Cho tam giác ABC có các đường phân giác trong là BE và CF cắt nhau tại M và các đường phân giác ngoài của các góc B và góc C cắt nhau tại N. Chứng minh tứ giác BMNC là tứ giác nội tiếp
Vẽ hình ra luôn
- mk ko bít
- ????
- tự làm nhé ^_^ !
a) BS, BE là phân giác của hai góc kề bù nên góc SBE =900
tương tự góc SCE = 900 => tứ giác BSCE nội tiếp
b) góc ASB = \(180^0-\left(gocBAS+gocABS\right)\)(tổng 3 góc trog tg ASB)
=> góc ASB = \(180^0-\left(\frac{gócABC}{2}+\frac{gocBAC}{2}\right)=180^0-\frac{gocABC+gocBAC}{2}\)
= \(180^0-\frac{180^0-gocACB}{2}=90^0+\frac{gocACB}{2}\) (1)
Ta lại có : góc BSE = 900 - góc BES mà góc BES = góc BCS( BSCE nội tiếp) ; góc BCS = góc ACB/2 => góc BES = góc ACB/2
=> góc BSE = \(90^0-\frac{gócACB}{2}\)(2)
từ (1) và (2) => góc ASB + góc BSE = 1800. Vậy A, S, E thẳng hàng