Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
\(\frac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}\)= \(\frac{2y}{3\left(x+y\right)^2}\)
\(\frac{x^2+2x+1}{5x^3+5x^2}=\frac{\left(x+1\right)^2}{5x^2\left(x+1\right)}=\frac{x+1}{5x^2}\)

a)\(\frac{\left(x+1\right)^2}{5x^2\left(x+1\right)}\)=\(\frac{x+1}{5x^2}\)
b)\(\frac{10y}{15\left(x+y\right)^2}\)

Ta có
\(\frac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}\)= \(\frac{2y}{3\left(x+y\right)^2}\)
\(\frac{7x^2+14x+7}{3x^2+3x}=\frac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\frac{7\left(x+1\right)}{3x}\)

Với đk trên ta có:
P = \(\frac{2}{x}-\left(\frac{x^2}{x^2+xy}+\frac{y^2-x^2}{xy}-\frac{y^2}{xy+y^2}\right).\frac{x+y}{x^2+xy+y^2}\)
\(=\frac{2}{x}-\left(\frac{x}{x+y}-\frac{\left(x-y\right)\left(x+y\right)}{xy}-\frac{y}{x+y}\right).\frac{x+y}{x^2+xy+y^2}\)
\(=\frac{2}{x}-\left(\frac{x-y}{x+y}-\frac{\left(x-y\right)\left(x+y\right)}{xy}\right).\frac{x+y}{x^2+xy+y^2}\)
\(=\frac{2}{x}-\frac{x-y}{xy}.\left(xy-\left(x+y\right)^2\right).\frac{1}{x^2+xy+y^2}\)
\(=\frac{2}{x}+\frac{x-y}{xy}\)
\(=\frac{x+y}{xy}\)

ĐKXĐ : \(x,y\ne0\)\(;\)\(x\ne y\)
\(a)\) \(P=\frac{2}{x}-\left(\frac{x^2}{x^2-xy}+\frac{x^2-y^2}{xy}-\frac{y^2}{y^2-xy}\right):\frac{x^2-xy+y^2}{x-y}\)
\(P=\frac{2}{x}-\left(\frac{x^2y}{xy\left(x-y\right)}+\frac{\left(x-y\right)^2\left(x+y\right)}{xy\left(x-y\right)}+\frac{xy^2}{xy\left(x-y\right)}\right):\frac{x^2-xy+y^2}{x-y}\)
\(P=\frac{2}{x}-\left(\frac{xy\left(x+y\right)+\left(x-y\right)^2\left(x+y\right)}{xy\left(x-y\right)}\right):\frac{x^2-xy+y^2}{x-y}\)
\(P=\frac{2}{x}-\frac{\left(x+y\right)\left(x^2-xy+y^2\right)}{xy\left(x-y\right)}.\frac{x-y}{x^2-xy+y^2}\)
\(P=\frac{2y}{xy}-\frac{x+y}{xy}=\frac{y-x}{xy}\)
\(b)\)
+) Với \(\left|2x-1\right|=1\)\(\Leftrightarrow\)\(\orbr{\begin{cases}2x-1=1\\2x-1=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=0\end{cases}}}\)
Mà \(x\ne0\) ( ĐKXĐ ) nên \(x=1\)
+) Với \(\left|y+1\right|=\frac{1}{2}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}y+1=\frac{1}{2}\\y+1=\frac{-1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}y=\frac{-1}{2}\\y=\frac{-3}{2}\end{cases}}}\)
Thay \(x=1;y=\frac{-1}{2}\) vào \(A=\frac{y-x}{xy}\) ta được : \(A=\frac{\frac{-1}{2}-1}{1.\frac{-1}{2}}=\frac{\frac{-3}{2}}{\frac{-1}{2}}=3\)
Thay \(x=1;y=\frac{-3}{2}\) vào \(A=\frac{y-x}{xy}\) ta được : \(A=\frac{\frac{-3}{2}-1}{1.\frac{-3}{2}}=\frac{\frac{-5}{2}}{\frac{-3}{2}}=\frac{15}{4}\)
Vậy ...
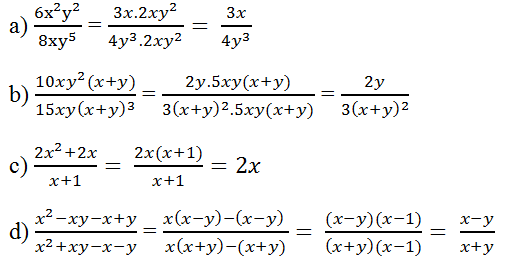
\(\frac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}\)
\(=\frac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)\left(x+y\right)^2}\)
\(=\frac{10y}{15\left(x+y\right)^2}\)
\(\frac{x^2-xy-x+y}{x^2+xy-x-y}\)
\(=\frac{\left(x^2-x\right)-\left(xy-y\right)}{\left(x^2-x\right)+\left(xy-y\right)}\)
\(=\frac{x\left(x-1\right)-y\left(x-1\right)}{x\left(x-1\right)+y\left(x-1\right)}\)
\(=\frac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}\)
\(=\frac{x-y}{x+y}\)
a)\(\frac{2xy}{3\left(x+y\right)^2}\)
b)=\(\frac{\left(x^2-xy\right)-\left(x-y\right)}{\left(x^2+xy\right)-\left(x+y\right)}\)=\(\frac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}\)
=\(\frac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}\)=\(\frac{\left(x-y\right)}{\left(x+y\right)}\)