Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lập phương trình
Gọi số trang là: x {hỏi cái gì đắt cái đó làm ẩn}
gọi số trang đọc theo đọc được theo từng ngày là: a[1,2,3]
thì ta có hệ phương trình:\(\left\{\begin{matrix}a_1+5=\frac{1}{5}x\\a_2-7=\left(x-a_1\right)\\a_3=\frac{2}{5}\left[x-\left(a_1+a_2\right)\right]\\a_4=\frac{2}{3}\left[x-\left(a_1+a_2+a_3\right)\right]\end{matrix}\right.\)
Thiếu 1 pt: \(\left(a_1+a_2+a_3+a_4+41\right)=x\) {không vào sửa được-> viết ngoài hệ}
Như vậy ta có hệ 5 pt 5 ẩn => đủ để tìm x, (bạn tự làm)
đọc lại đề nhầm ngày thứ 4 đọc hết quyển truyện {tương còn để lại 41}
do vây--> a4=2/3[...]+41
Phuowfg trình bên ngoài hệ còn (a1+a2+a3+a4)=x

Chọn D
Lấy lần lượt 3 cuốn sách có 15.14.13 = 2730 cách
Lấy 2 cuốn sách đầu là Toán và cuốn còn lại là Văn có 10.9.5 = 450 cách
Xác suất để được hai cuốn sách đầu là Toán, cuốn thứ ba là Văn: ![]()

Để đặt cây thước kẻ \(a\) song song các trang của một cuốn sách, ta đặt nó song song với mép cuốn sách.

Nếu bạn mới học lớp 11 thì không cần quan tâm bài xác suất này.
Đây là xác suất phân phối của biến rời rạc nằm trong chương trình xác suất thống kê của đại học, phương pháp tính riêng (cần có bảng để tra) hoàn toàn ko liên quan đến xác suất của phổ thông
Lời giải:
Xác suất để quyển sách không lỗi trang nào:
\((1-0,002)^{1000}\)
Xác suất để quyển sách lỗi 1 trang:
\((1-0,002)^{999}.0,002.1000=2.0,998^{999}\)
Xác suất để quyển sách lỗi 2 trang là:
\((1-0,002)^{998}.0,002^2.C^2_{1000}\)
Cộng ba số trên ta có xác suất cần tìm.

Đáp án là A.
• Ta tìm số cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn.
Có 3 trường hợp :
• 7 cuốn còn lại gồm 2 môn toán lý : có C 9 7 cách
• 7 cuốn còn lại gồm 2 môn lý hóa : có C 11 7 cách
• 7 cuốn còn lại gồm 2 môn toán hóa : có C 10 7 cách
Suy ra có C 9 7 + C 11 7 + C 10 7 = 486 cách chọn 7 cuốn còn lại sao cho không có đủ 3 môn. Do đó số cách chọn 8 cuốn sao cho 7 cuốn còn lại có đủ 3 môn là C 15 7 - 486 = 5949 cách.
Xác suất cần tìm là P = 5949 C 15 7 = 661 715

Chọn C
Xét phép thử T: “Chọn 7 cuốn sách từ 15 cuốn sách”.
Số phần tử của không gian mẫu trong phép thử là C 15 7 .
Gọi A biến cố chọn 7 cuốn sách có đủ 3 môn trong phép thử T.
Xác suất của biến cố cần tìm bằng xác suất của biến cố A.
Ta có ![]()
Vậy
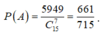

Đáp án B

Gọi biến cố A: “Số cuốn sách còn lại của thầy Tuấn có đủ cả ba môn”.
Khi đó ta có biến cố: A ¯ : “Số cuốn sách còn lại của thầy Tuấn không có đủ cả 3 môn”.


Tham khảo link:
Giải toán trên mạng - Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath