
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm

a: =>3^x*3+3^x=108
=>3^x=27
=>x=3
b: =>5^x*26=650
=>5^x=25
=>x=2
e: =>16x=2
=>x=1/8
g: =>14*7^x-7^x*5=441
=>9*7^x=441
=>7^x=49
=>x=2
h: =>\(\left(x-5\right)^{10}\left[\left(x-5\right)^2-1\right]=0\)
=>(x-5)(x-6)(x-4)=0
=>\(x\in\left\{5;6;4\right\}\)

\(b,=\left|\dfrac{17}{6}-\dfrac{35}{6}\right|+1=3+1=4\\ c,=\dfrac{7^3\left(7^2-4\right)}{45}=\dfrac{7^3\cdot45}{45}=7^3=343\)

a:
\(AB=\dfrac{AC}{2}\)
\(AD=DC=\dfrac{CA}{2}\)
Do đó: AB=AD=DC
Xét ΔAHB vuông tại H và ΔCED vuông tại E có
AB=CD(cmt)
\(\widehat{HAB}=\widehat{ECD}\left(=90^0-\widehat{HBA}\right)\)
Do đó: ΔAHB=ΔCED
b: DE\(\perp\)BC
AH\(\perp\)BC
Do đó: DE//AH
Xét ΔCAH có
D là trung điểm của AC
DE//AH
Do đó: E là trung điểm của CH
=>EC=EH
Xét ΔDHC có
DE là đường cao
DE là đường trung tuyến
Do đó: ΔDHC cân tại D
c: ΔABD vuông tại A
mà AI là đường trung tuyến
nên \(AI=\dfrac{1}{2}BD\left(1\right)\)
ΔBED vuông tại E
mà EI là đường trung tuyến
nên \(EI=\dfrac{1}{2}BD\left(2\right)\)
Từ (1) và (2) suy ra AI=EI
ΔAHB=ΔCED
=>AH=CE
mà CE=EH
nên AH=EH
XétΔAHI và ΔEHI có
HA=HE
HI chung
AI=EI
Do đó: ΔAHI=ΔEHI
d: Xét ΔIDE có ID=IE
nên ΔIDE cân tại I
IK//BC
BC\(\perp\)DE
Do đó: IK\(\perp\)DE
ΔIDE cân tại I
mà IK là đường cao
nên IK là phân giác của góc DIE
=>\(\widehat{DIK}=\widehat{EIK}\)
Xét ΔIKD và ΔIKE có
IK chung
\(\widehat{KID}=\widehat{KIE}\)
ID=IE
Do đó: ΔIKD=ΔIKE
f: Xét tứ giác ADEB có
\(\widehat{DAB}+\widehat{DEB}=90^0+90^0=180^0\)
=>ADEB là tứ giác nội tiếp
=>\(\widehat{AED}=\widehat{ABD}=45^0\)

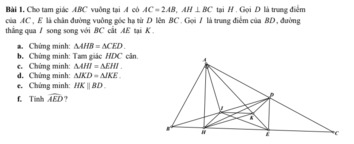
Bài 5:
\(\widehat{BKC}=180^0-\left(\widehat{KBC}+\widehat{KCB}\right)\)
\(=180^0-\dfrac{180^0-80^0}{2}\)
\(=180^0-50^0=130^0\)

\(a,\frac{5}{6}-2\sqrt{\frac{4}{9}}+\sqrt{\left(-2\right)^2}\)
\(=\frac{5}{6}-2.\frac{2}{3}+2\)
\(=\frac{5}{6}-\frac{4}{6}+\frac{12}{6}\)
\(=\frac{5-4+12}{6}=\frac{13}{6}\)
\(b,\left(-3\right)^2.\left(\frac{1}{3}\right)^3:\left[\left(-\frac{2}{3}\right)^3-1\frac{1}{3}\right]-\left(-200\right)^0\)
\(=9.\frac{1}{27}:\left(-\frac{8}{27}-\frac{5}{3}\right)-1\)
\(=\frac{1}{3}:\left(-\frac{8}{27}-\frac{45}{27}\right)-1\)
\(=\frac{1}{3}:\left(-\frac{53}{27}\right)-1\)
\(=\frac{1}{3}.\left(-\frac{27}{53}\right)-1\)
\(=-\frac{9}{53}-1=-\frac{9}{53}-\frac{53}{53}\)
\(=-\frac{62}{53}\)
\(c,\left(-0,5-\frac{3}{5}\right):\left(-3\right)+\frac{1}{3}-\left(-\frac{1}{6}\right):2\)
\(=\left(-\frac{1}{2}-\frac{3}{5}\right).\frac{1}{3}+\frac{1}{3}-\left(-\frac{1}{6}\right).\left(-\frac{1}{2}\right)\)
\(=\left(-\frac{5}{10}-\frac{6}{10}\right).\frac{1}{3}+\frac{1}{3}-\frac{1}{12}\)
\(=-\frac{11}{10}.\frac{1}{3}+\frac{1}{3}-\frac{1}{12}\)
\(=\frac{1}{3}\left(-\frac{11}{10}-\frac{1}{12}\right)\)
\(=\frac{1}{3}\left(-\frac{66}{60}-\frac{5}{60}\right)\)
\(=\frac{1}{3}.\left(-\frac{71}{60}\right)\)
\(=-\frac{71}{180}\)

Bài 4:
Gọi số sách vở khối 6,7,8,9 quyên góp lần lượt là a,b,c,d(quyển)(a,b,c,d∈N*)
Áp dụng t/c dtsbn:
\(\dfrac{a}{8}=\dfrac{b}{7}=\dfrac{c}{6}=\dfrac{d}{5}=\dfrac{a-c}{8-6}=\dfrac{80}{2}=40\)
\(\Rightarrow\left\{{}\begin{matrix}a=40.8=320\\b=40.7=280\\c=40.6=240\\d=40.5=200\end{matrix}\right.\)(nhận)
Vậy...
Bài 5:
Gọi số giấy vụn của lớp 8,7,6 lần lượt là a,b,c(kg)(a,b,c>0)
Áp dụng t/c dtsbn:
\(\dfrac{a}{7}=\dfrac{b}{8}=\dfrac{c}{9}=\dfrac{c-a}{9-7}=\dfrac{80}{2}=40\)
\(\Rightarrow\left\{{}\begin{matrix}a=40.7=280\\b=40.8=320\\c=40.9=360\end{matrix}\right.\)(nhận)
Vậy...

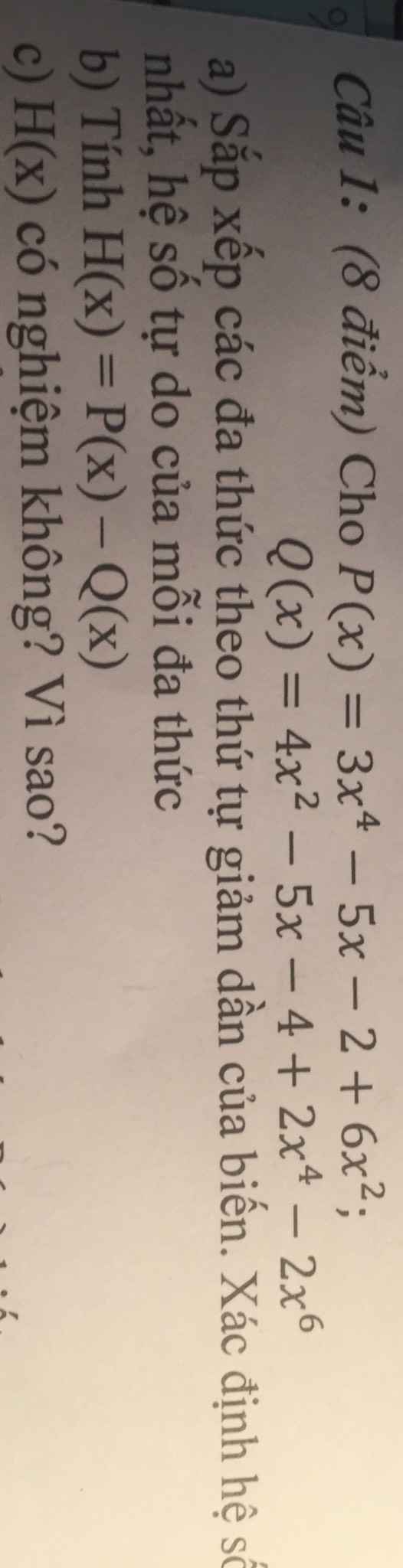
 giúp mình (không cần làm câu c, f, d)
giúp mình (không cần làm câu c, f, d)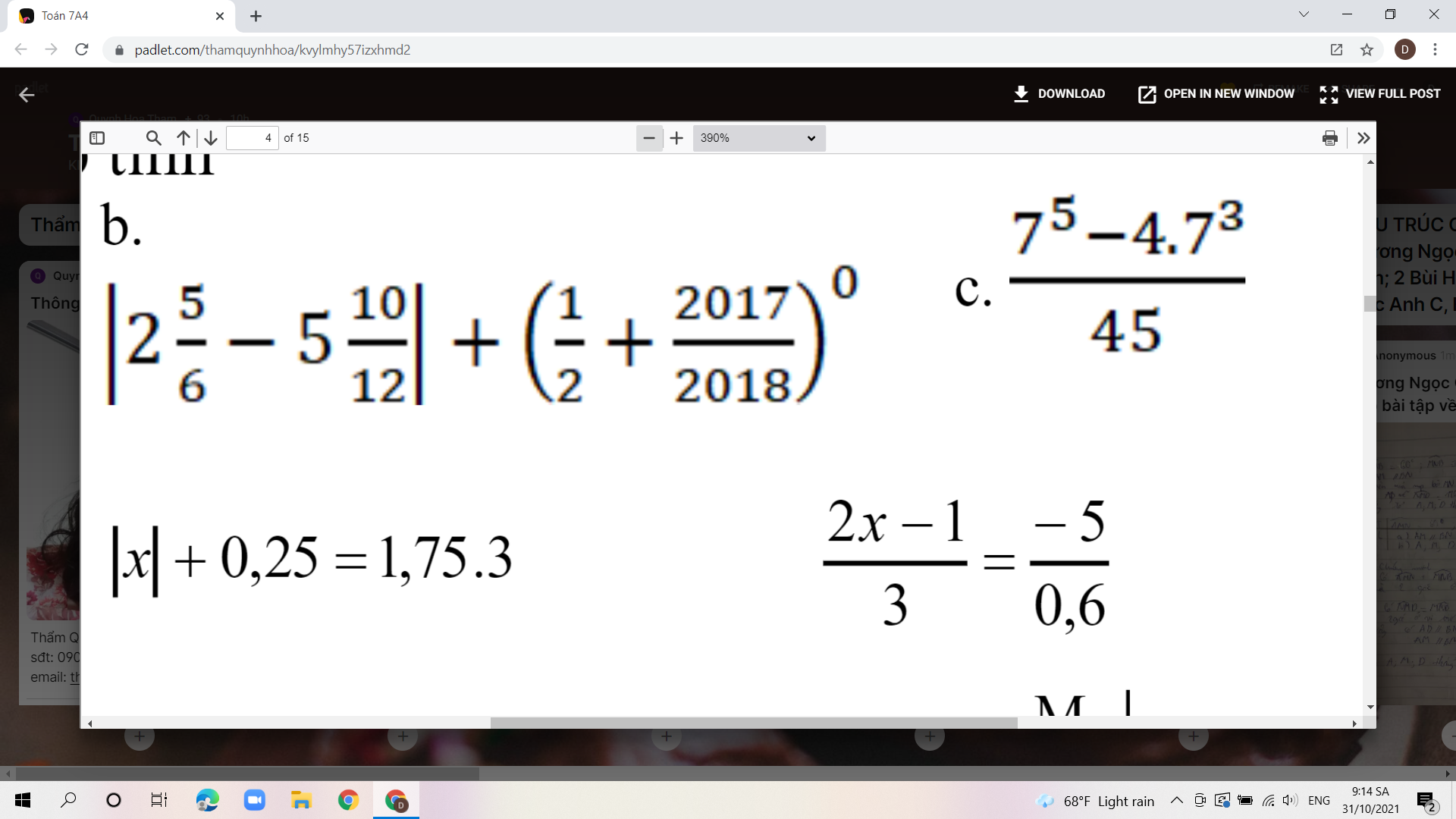
 Mọi người ơi làm giúp mình nha (làm 1 câu cũng được, 2 câu cũng được, mình tick tất nha)
Mọi người ơi làm giúp mình nha (làm 1 câu cũng được, 2 câu cũng được, mình tick tất nha)

Answer:
\(\left(\frac{-1}{2}\right)^2.\left(-\sqrt{16}\right)+\left(\frac{-2021}{2022}\right)^0+\sqrt{\frac{9}{25}}:\left|-\frac{3}{20}\right|.\left(-1\right)^{2021}\)
\(=\frac{1}{4}.\left(-4\right)+1+\frac{3}{5}:\frac{3}{20}.\left(-1\right)\)
\(=-1+1-\frac{3}{5}.\frac{20}{3}\)
\(=0-\frac{20}{5}\)
\(=-4\)