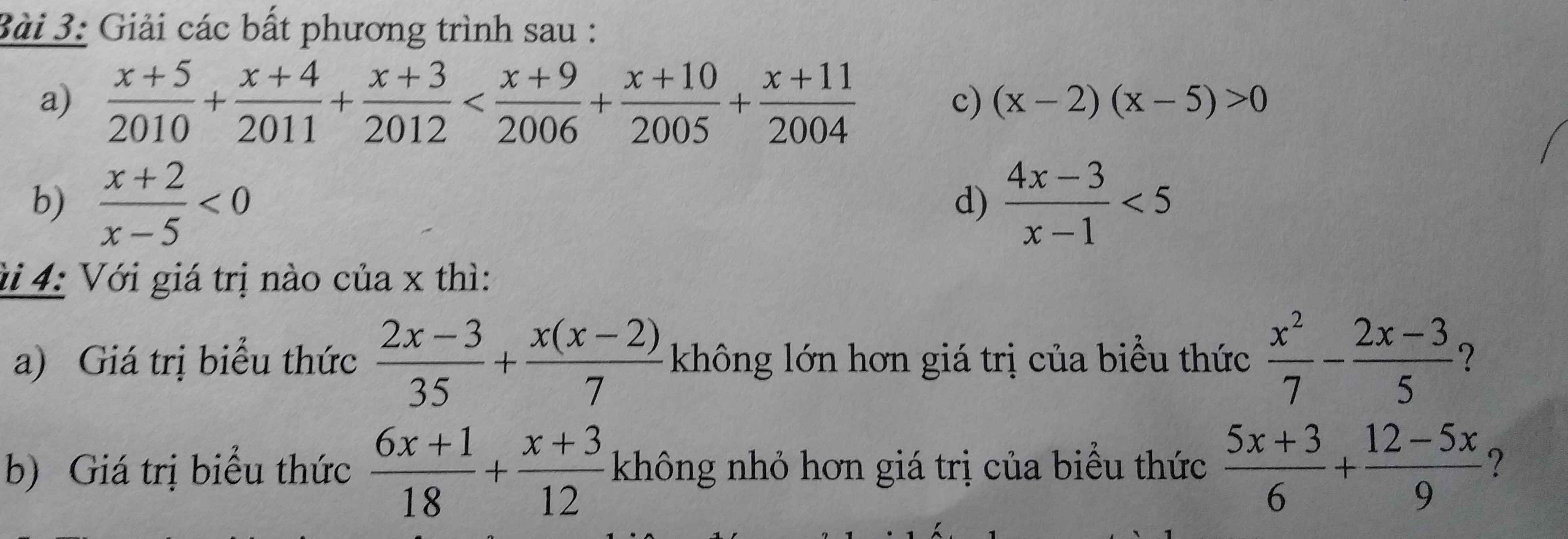K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
Nguyễn Minh Quang
Giáo viên
3 tháng 9 2021
xét mọi số chính phương đều có thể viết dưới dạng :
\(\left(a\cdot n+b\right)^2\) với mọi số \(a,b\) là các số tự nhiên và b nhở hơn n
mà ta có :
\(\left(a\cdot n+b\right)^2=a^2\cdot n^2+2ab\cdot n+b^2\equiv b^2mod\left(n\right)\)
vậy \(b^2< n\forall b< n\)điều này chỉ đúng khi n=2
vậy n=2
MH
29 tháng 2 2016
PT <=> \(2x+\frac{6}{5}=5-\frac{13}{5}-x\)
<=> \(\frac{10x+6}{5}=\frac{25}{5}-\frac{13}{5}-\frac{5x}{5}\)
=> 10x + 6 = 25 - 13 - 5x
<=> 10x + 5x = 25 - 13 - 6
<=> 15x = 6
<=> x = 2/5
Vậy S = {2/5}.
29 tháng 2 2016
\(2\left(x+\frac{3}{5}\right)=5-\left(\frac{13}{5}+x\right)\)
<=> \(2x+\frac{6}{5}=\frac{12}{5}-x\)
<=> \(3x=\frac{6}{5}\) <=> \(x=\frac{2}{5}\)
TT
3
KH
6 tháng 3 2016
GTLN = 17/8 tại x = 3/4
Chuẩn không cần chỉnh (ai tích mình mình tích lại)
6 tháng 3 2016
-(2x2-3x-1)=\(-2\left(x^2-\frac{3}{2}x-1\right)\)
=\(-2\left(x^2-2.\frac{3}{4}x+\frac{9}{16}-\frac{25}{16}\right)=-2\left(x-\frac{3}{4}\right)+\frac{25}{3}\)
vật gtln là 25/3 khi x=3/4
VH
0
5 tháng 10 2021
bạn tự vẽ hình nha
giải
a) K là trung điểm EM
H là trung điểm ED
=> KH là đường trung bình của \(\Delta\) EMD ( đpcm)
b) KH là đường trung bình \(\Delta EMD\)
\(\Rightarrow\) KH = \(\dfrac{1}{2}MD\)
\(\Rightarrow MD=2.KH\Rightarrow MD=2.20=40\) ( cm)
c) KH là đường trung bình \(\Delta EMD\)
\(\Rightarrow\) KH // MD (1)
\(\Delta EMD\) cân \(\Rightarrow\) \(\widehat{M}=\widehat{D}\) (2)
từ (1) và (2) tứ giác KHDM là hình thang cân ( đpcm )
5 tháng 10 2021
a: Xét ΔEMD có
K là trung điểm của EM
H là trung điểm của ED
Do đó: KH là đường trung bình của ΔEMD
b: \(MD=2\cdot KH=2\cdot20=40\left(cm\right)\)
c: Xét tứ giác MKHD có HK//MD
nên MKHD là hình thang
mà \(\widehat{M}=\widehat{D}\)
nên MKHD là hình thang cân
23 tháng 6 2023
3
a: =>\(\left(\dfrac{x+5}{2010}+1\right)+\left(\dfrac{x+4}{2011}+1\right)+\left(\dfrac{x+3}{2012}+1\right)< \left(\dfrac{x+9}{2006}+1\right)+\left(\dfrac{x+10}{2005}+1\right)+\left(\dfrac{x+11}{2004}+1\right)\)
=>x+2015<0
=>x<-2015
b: =>x+2>0 và x-5<0
=>-2<x<5
c: =>x-5>0 hoặc x-2<0
=>x<2 hoặc x>5
d: =>(4x-3-5x+5)/(x-1)<0
=>(-x+2)/(x-1)<0
=>(x-2)/(x-1)>0
=>x>2 hoặc x<1