
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



mình giải khác @Aliba -@Aliba phân tích thành nhân tử. Mình làm bình thường nhân phân phối
\(\left(1\right)\Leftrightarrow x^2-\left(3y+2\right)x+2y^2+4y=0\)coi như hàm bậc 2 với x giải bình thường
\(\Delta\left(x\right)=\left(3y+2\right)^2-4\left(2y^2+4y\right)=\left(y-2\right)^2\) nhận phân phối ra giản ước là xong
\(\orbr{\begin{cases}x=\frac{3y+2-\left(y-2\right)}{2}=y+2\\x=\frac{3y+2+\left(y-2\right)}{2}=2y\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}y=x-2\\y=\frac{x}{2}\end{cases}}\) thấy y theo x không dúng x thấy y vào (2)
\(\left(2\right)\Leftrightarrow\orbr{\begin{cases}\left(x^2-5\right)^2=2x-2\left(x-2\right)+5\\\left(x^2-5\right)=2x-2.\frac{x}{2}+5\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\left(x^2-5\right)^2=9\left(3\right)\\\left(x^2-5\right)^2=\left(x+5\right)\left(4\right)\end{cases}}\)
\(\left(3\right)\Leftrightarrow\orbr{\begin{cases}x_{1,2}=+-\sqrt{2}\\x_{3,4}=+-2\sqrt{2}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}y_{1,2}=+-\sqrt{2}-2\\y_{3,4}=+-2\sqrt{2}-2\end{cases}}\)
\(\left(4\right)\Leftrightarrow x^4-10x^2-x+20=0\)\(\Leftrightarrow\left(x^2-ax+b\right)\left(x^2+ax+c\right)\)đồng nhất hệ số \(\hept{\begin{cases}a=1\\b=-5\\c=-4\end{cases}}\)
\(\left(4\right)\Leftrightarrow\left(x^2-x-5\right)\left(x^2+x-4\right)=0\)
\(\hept{\begin{cases}x^2-x-5=0\\x^2+x-4=0\end{cases}}\)\(\orbr{\begin{cases}\Delta=21\\\Delta=17\end{cases}}\)
\(\orbr{\begin{cases}x_{5,6}=\frac{1+-\sqrt{21}}{2}\\x_{7,8}=\frac{-1+-\sqrt{17}}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}y_{5,6}=\frac{1+-\sqrt{21}}{4}\\y_{7,8}=\frac{-1+-\sqrt{17}}{4}\end{cases}}\)
\(\hept{\begin{cases}x^2+2y^2-3xy-2x+4y=0\left(1\right)\\\left(x^2-5\right)^2=2x-2y+5\left(2\right)\end{cases}}\)
Xét \(\left(1\right)\Leftrightarrow\left(x^2-2xy\right)+\left(2y^2-xy\right)+\left(-2x+4y\right)=0\)
\(\Leftrightarrow\left(x-2y\right)\left(x-y-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=2y\\x=2+y\end{cases}}\)
Thế x = 2y vào (2) ta được
\(\left(4y^2-5\right)^2=4y-2y+5\)
\(\Leftrightarrow16y^4-40y^2-2y+20=0\)
\(\Leftrightarrow8y^4-20y^2-y+10=0\)
\(\Leftrightarrow\left(8y^4+4y^3-8y^2\right)+\left(-4y^3-2y^2+4y\right)+\left(-10y^2-5y+10\right)=0\)
\(\Leftrightarrow\left(2y^2+y-2\right)\left(4y^2-2y-5\right)=0\)
Tới đây thì đơn giản rồi. Cái còn lại làm tương tự

(x^2+6x+5)(x^2+6x+8)=10
Đặt x^2+6x+5=a>>>(a+3)a=10
a^2+3a-10=0 >>>(a+5)(a-2)=0>>>a=-5 hoặc a=2
Đến đây thay a =x^2+6x+5 ròi giải

5:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
b: \(MA=\sqrt{OM^2-OA^2}=R\sqrt{3}\)
=>\(AH=\dfrac{R\cdot R\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
=>\(AB=R\sqrt{3}\)

Bài 5:
a) Ta có: \(A=\left(\dfrac{4x+5\sqrt{x}-1}{x\sqrt{x}+2x-\sqrt{x}-2}-\dfrac{3\sqrt{x}+1}{x+\sqrt{x}-2}\right):\dfrac{x+4\sqrt{x}+4}{x-1}\)
\(=\left(\dfrac{4x+5\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(3\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4x+5\sqrt{x}-1-3x-3\sqrt{x}-\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)^3}\)
\(=\dfrac{\sqrt{x}-1}{x+4\sqrt{x}+4}\)
b) Ta có: \(A-1=\dfrac{\sqrt{x}-1-x-4\sqrt{x}-4}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+3\sqrt{x}+5\right)}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+2\cdot\sqrt{x}\cdot\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{11}{4}}{x+4\sqrt{x}+4}< 0\forall x\) thỏa mãn ĐKXĐ
nên A<1

Câu 5:
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔCED nội tiếp
CD là đường kính
Do đó; ΔCED vuông tại E
=>CE\(\perp\)ED tại E
=>CE\(\perp\)AD tại E
Xét ΔDCA vuông tại C có CE là đường cao
nên \(DA\cdot DE=DC^2=\left(2R\right)^2=4R^2\left(3\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(4\cdot OH\cdot OA=4\cdot OB^2=\left(2OB\right)^2=4R^2\left(4\right)\)
Từ (3) và (4) suy ra \(DA\cdot DE=4\cdot OH\cdot OA\)

3.
a, \(\sqrt{18x}=3\sqrt{2x}\)
b, \(\sqrt{75x^2y}=5\left|x\right|\sqrt{3y}\)
c, \(11\left|xy\right|\sqrt{5x}\)

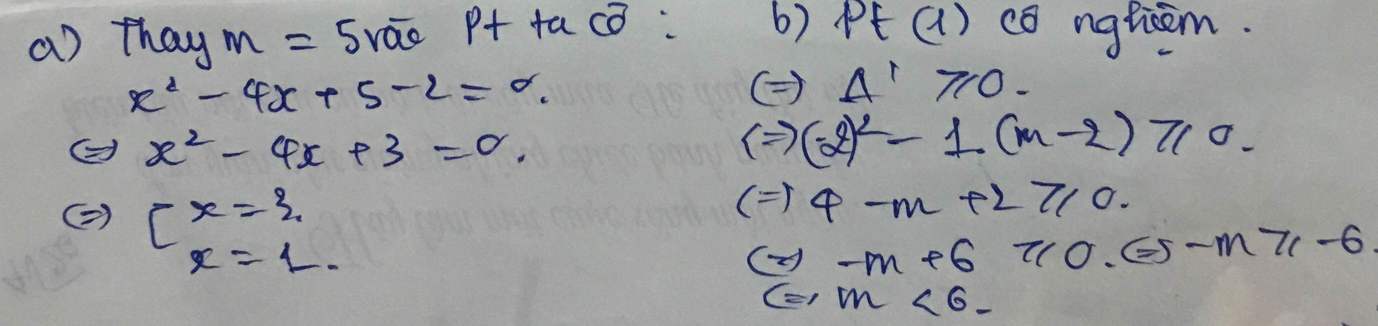
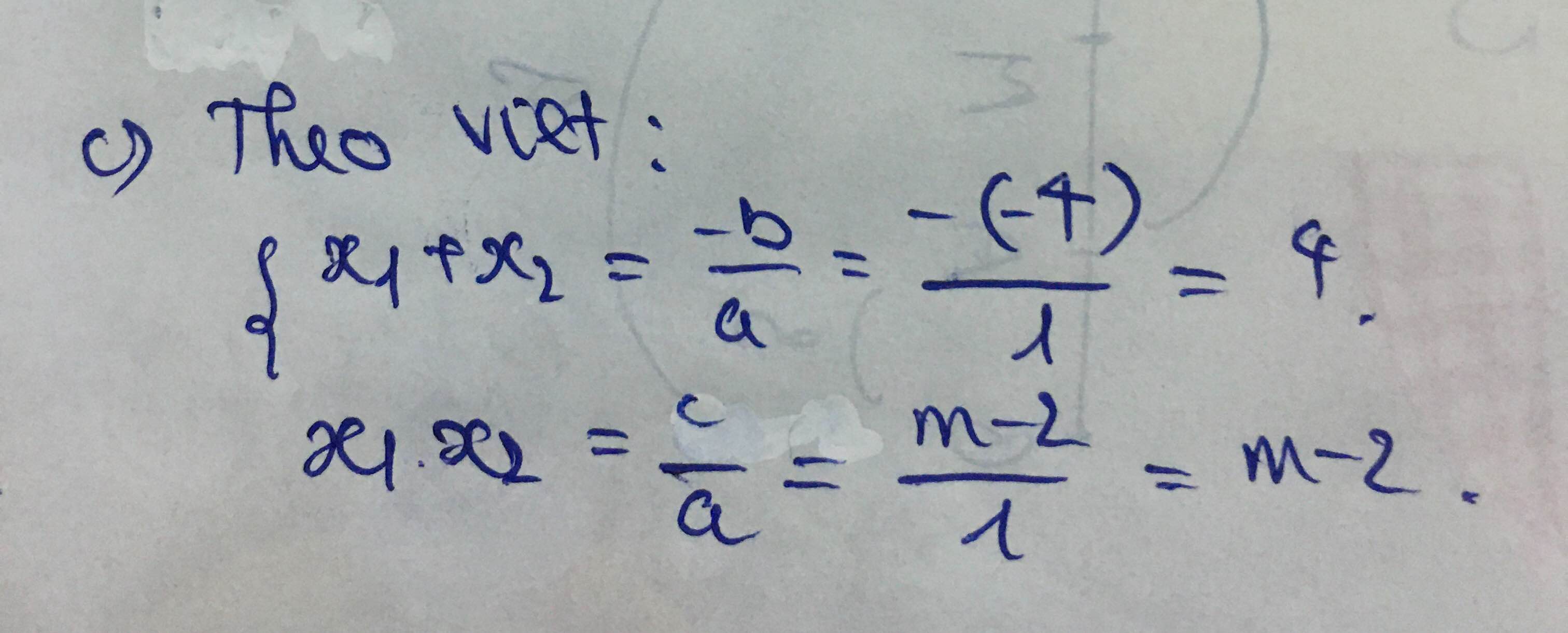

 giúp mình câu c4 và câu 5 với
giúp mình câu c4 và câu 5 với giúp mình câu b bài 5 vs câu b bài 6 đi
giúp mình câu b bài 5 vs câu b bài 6 đi
 giúp mình câu 5 với ạ
giúp mình câu 5 với ạ
Thiếu đề