
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


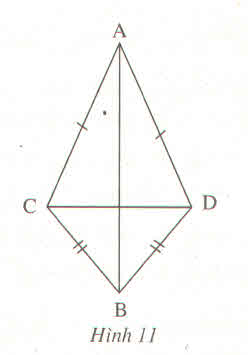
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD

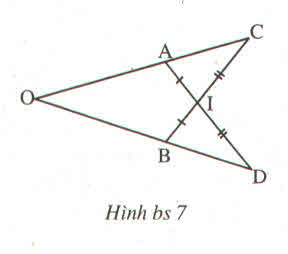
Xét tam giác IAC và IBD có:
IA = IB ( theo đề bài)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( theo đề bài )
Do đó: tam giác IAC = tam giác IBD (c.g.c)
Suy ra góc ACI = góc BDI ( 2 góc tương ứng) \(\left(1\right)\)
Suy ra góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = \(180^0\)(2 góc kề bù)
góc OBI + góc IBD = \(180^0\)(2 góc kề bù)
mà: góc IAC = góc IBD (*)
Suy ra góc: OAI = góc OBI (5)
Xét tam giác: OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
Do đó: tam giác OAD = tam giác OBC (g.c.g)
Suy ra: OA = OB (2 cạnh tương ứng)
Xét tam giác IAC và tam giác IBD có:
IA = IB ( gt)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( gt )
=> Tam giác IAC = tam giác IBD (c.g.c)
=> Góc ACI = góc BDI ( 2 góc tương ứng) (1)
và góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = 1800 (2 góc kề bù)
góc OBI + góc IBD = 1800 (2 góc kề bù)
mà: góc IAC = góc IBD (*)
=> góc: OAI = góc OBI (5)
Xét tam giác OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
=> Tam giác OAD = tam giác OBC (g.c.g)
=> OA = OB (2 cạnh tương ứng)

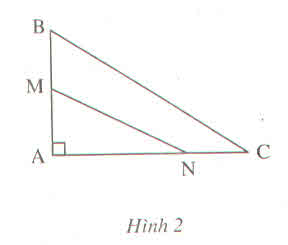
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.

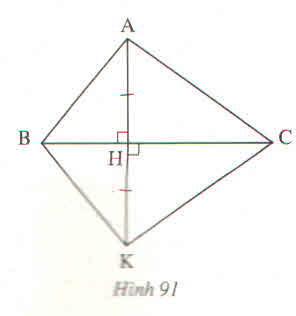
Giải:
∆AHB và ∆KBH có
AH=KH(gt)
\(\widehat{AHB}\)=\(\widehat{KHM}\)
BH cạnh chung .
nên ∆AHB=∆KBH(c.g.c)
suy ra: \(\widehat{ABH}\)=\(\widehat{KBH}\)
Vậy BH là tia phân giác của góc B.
Tương tự ∆AHC =∆KHC(c.g.c)
Suy ra: \(\widehat{ACH}\)=\(\widehat{KCH}\)
Vậy CH là tia phân giác của góc C.













16.
\(A=\dfrac{16^2.16^3}{4^8}=\dfrac{4^4.4^6}{4^8}=\dfrac{4^{10}}{4^8}=4^2=16\)
\(B=\dfrac{8^2.8^3}{2^{11}}=\dfrac{2^6.2^9}{2^{11}}=\dfrac{2^{15}}{2^{11}}=2^4=16\)
17.
\(6,673\)
18.
\(\Rightarrow x=\dfrac{-3}{5}.15=-9\)
19.
\(x=12:\dfrac{3}{4}=16\)
20.Áp dụng t/c dtsbn ta có;
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{x+y}{8+12}=\dfrac{40}{20}=2\)
\(\dfrac{x}{8}=2\Rightarrow x=16\\ \dfrac{y}{12}=2\Rightarrow y=24\)
21.
Áp dụng t/c dtsbn ta có;
\(\dfrac{x}{4}=\dfrac{y}{9}=\dfrac{x-y}{4-9}=\dfrac{15}{-5}=-3\)
\(\dfrac{x}{4}=-3\Rightarrow x=-12\\ \dfrac{y}{9}=-3\Rightarrow y=-27\)
22.
gọi số học sinh nam, nữ lần lượt là a,b
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{6}=\dfrac{b}{7}\\a+b=39\end{matrix}\right.\)
Áp dụng t/c dtsbn ta có;
\(\dfrac{a}{6}=\dfrac{b}{7}=\dfrac{a+b}{6+7}=\dfrac{39}{13}=3\)
\(\dfrac{a}{6}=3\Rightarrow a=18\\ \dfrac{b}{7}=3\Rightarrow b=21\)
Vậy ...
23.\(\sqrt{16}=4\)
24.\(\sqrt{x}=5\Rightarrow x=25\)
25.B
26.A
Còn câu 22,23,24,25,26