
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Theo mk được biết thì Shinichi và Kid là hai anh em nên mk thích cả hai

\(\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{99}{100}}\\ =\dfrac{200-\left(2+1+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{\left(1-\dfrac{1}{2}\right)+\left(1-\dfrac{1}{3}\right)+\left(1-\dfrac{1}{4}\right)+...+\left(1-\dfrac{99}{100}\right)}\\ =\dfrac{200-2-1-\dfrac{2}{3}-\dfrac{2}{4}-\dfrac{2}{5}-...-\dfrac{2}{100}}{\left(1+1+1+...+1\right)-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{198-\left(\dfrac{2}{2}+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{2\cdot99-2\cdot\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =\dfrac{2\cdot\left[99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\right]}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)}\\ =2\)
Đề nhỏ quá!! mà t 4 mắt. cẩn thận
Đặt :
\(A=\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+.............+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+....................+\dfrac{99}{100}}\)
\(A=\dfrac{200-2-\left(\dfrac{2}{2}+\dfrac{2}{3}+\dfrac{2}{4}+..............+\dfrac{2}{100}\right)}{1-\dfrac{1}{2}+1-\dfrac{1}{3}+.................+1-\dfrac{1}{100}}\)
\(A=\dfrac{198-\left(\dfrac{2}{2}+\dfrac{2}{3}+..................+\dfrac{2}{100}\right)}{\left(1+1+.....+1\right)-\left(\dfrac{1}{2}+\dfrac{1}{3}+...........+\dfrac{1}{100}\right)}\)
\(A=\dfrac{2\left[99-\left(\dfrac{1}{2}+\dfrac{1}{3}+.............+\dfrac{1}{100}\right)\right]}{99-\left(\dfrac{1}{2}+\dfrac{1}{3}+..............+\dfrac{1}{100}\right)}\)
\(A=2\)
Vậy \(\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+............+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...............+\dfrac{99}{100}}=2\rightarrowđpcm\)


Ta có: \(\dfrac{1}{2}\cdot y+\dfrac{2}{3}\cdot y=\dfrac{7}{6}\Rightarrow y\left(\dfrac{1}{2}+\dfrac{2}{3}\right)=\dfrac{7}{6}\Rightarrow\dfrac{7}{6}y=\dfrac{7}{6}\Rightarrow y=\dfrac{7}{6}:\dfrac{7}{6}=1\)
Vậy \(D=\left\{1\right\}\)
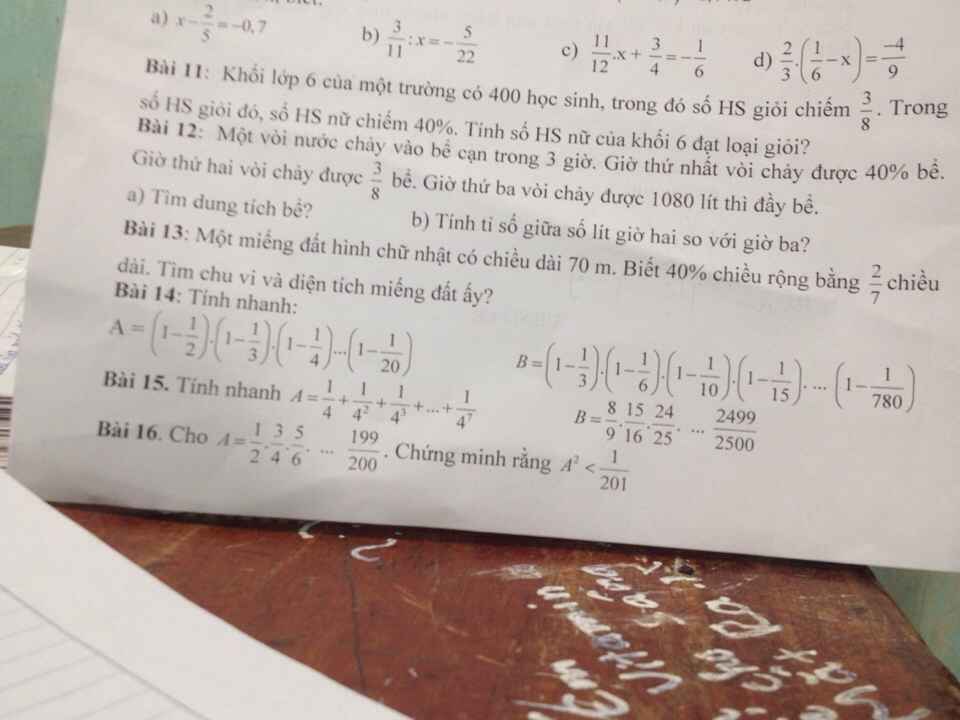




 Mình cảm ơn ạ
Mình cảm ơn ạ






 giúp tớ với
giúp tớ với


B16:
Biểu thức C là tích của 100 phân số nhỏ hơn 1 , trong đó các tử đều lẽ , các mẫu đều chẵn . Ta đưa ra biểu thức trung gian là một tích các phân số mà tử số các phân số đều chẵn và mẫu số các phân số đều lẽ . Thêm 1 vào tử và mẫu của mỗi phân số của A , giá trị mỗi phân số tăng lên , do đó:
ta có:
\(A< \dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\left(1\right)\)
\(A< \dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\left(2\right)\)
Nhân (1) vs (2) theo từng vế ta được:
\(A^2< \left(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.....\dfrac{199}{200}\right).\left(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{200}{201}\right)\)
Vế phải của bđt trên bằng \(\dfrac{1}{201}\)
Vậy \(A^2< \dfrac{1}{201}\left(đpcm\right)\)
15.
\(A=\dfrac{1}{4}+\dfrac{1}{4^2}+...+\dfrac{1}{4^7}\)
\(4A=1+\dfrac{1}{4}+...+\dfrac{1}{4^6}\)
\(\Rightarrow4A-A=1-\dfrac{1}{4^7}\)
\(\Rightarrow3A=1-\dfrac{1}{4^7}\)
\(\Rightarrow A=\dfrac{1}{3}\left(1-\dfrac{1}{4^7}\right)\)
\(B=\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}=\dfrac{2.4}{3^2}.\dfrac{3.5}{4^2}...\dfrac{49.51}{50^2}\)
\(B=\dfrac{2.3...49}{3.4...50}.\dfrac{4.5...51}{3.4...50}=\dfrac{2}{50}.\dfrac{51}{3}=\dfrac{17}{25}\)