Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
Đặt \(a = \frac{1}{x} ; b = \frac{1}{y} ; c = \frac{1}{z} \Rightarrow x y z = 1\) và \(x ; y ; z > 0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P = \frac{1}{\frac{1}{x^{3}} \left(\right. \frac{1}{y} + \frac{1}{z} \left.\right)} + \frac{1}{\frac{1}{y^{3}} \left(\right. \frac{1}{z} + \frac{1}{x} \left.\right)} + \frac{1}{\frac{1}{z^{3}} \left(\right. \frac{1}{x} + \frac{1}{y} \left.\right)}\)
\(= \frac{x^{3} y z}{y + z} + \frac{y^{3} z x}{z + x} + \frac{z^{3} x y}{x + y} = \frac{x^{2}}{y + z} + \frac{y^{2}}{z + x} + \frac{z^{2}}{x + y}\)
\(P \geq \frac{\left(\left(\right. x + y + z \left.\right)\right)^{2}}{y + z + z + x + x + y} = \frac{x + y + z}{2} \geq \frac{3 \sqrt[3]{x y z}}{2} = \frac{3}{2}\)
\(P_{m i n} = \frac{3}{2}\) khi \(x = y = z = 1\) hay \(a = b = c = 1\)

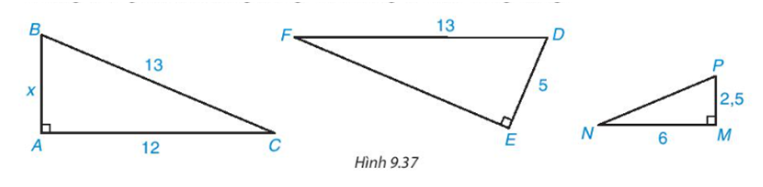
\({x^2} = {4^2} + {2^2} = 20 \Rightarrow x = 2\sqrt 5 \)
\({y^2} = {5^2} - {4^2} = 9 \Leftrightarrow y = 3\)
\({z^2} = {\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2} = 25 \Rightarrow z = 5\)
\({t^2} = {1^2} + {2^2} = 5 \Rightarrow t = \sqrt 5 \)

Những tam giác đồng dạng là
- Tam giác ABC đồng dạng với tam giác EDF với tỉ số đồng dạng là 1
- Tam giác MPN đồng dạng với tam giác ABC với tỉ số đồng dạng là \(\frac{1}{2}\)
- Tam giác MPN đồng dạng với tam giác EDF với tỉ số đồng dạng là \(\frac{1}{2}\)

Bài 13:
a: \(\left\lbrack5\left(x-2y\right)^3\right\rbrack:\left(5x-10y\right)\)
\(=\frac{5\left(x-2y\right)^3}{5\cdot\left(x-2y\right)}\)
\(=\left(x-2y\right)^2\)
b: \(\left\lbrack5\left(a-b\right)^3+2\left(a-b\right)^2\right\rbrack:\left(b-a\right)^2\)
\(=\frac{5\left(a-b\right)^3+2\left(a-b\right)^2}{\left(a-b\right)^2}\)
\(=\frac{5\left(a-b\right)^3}{\left(a-b\right)^2}+\frac{2\left(a-b\right)^2}{\left(a-b\right)^2}\)
=5(a-b)+2
c: Sửa đề: \(\left(x^3+8y^3\right):\left(x+2y\right)\)
\(=\frac{\left(x+2y\right)\left(x^2-2xy+4y^2\right)}{x+2y}\)
\(=x^2-2xy+4y^2\)
Bài 11:
a: Gọi ba số tự nhiên liên tiếp lần lượt là a;a+1;a+2
Tích của hai số sau lớn hơn tích của hai số đầu là 52 nên ta có:
\(\left(a+1\right)\left(a+2\right)-a\left(a+1\right)=52\)
=>\(\left(a+1\right)\left(a+2-a\right)=52\)
=>2(a+1)=52
=>a+1=26
=>a=25
Vậy: ba số tự nhiên liên tiếp cần tìm là 25;25+1=26; 25+2=27
b: a chia 5 dư 1 nên a=5x+1
b chia 5 dư 4 nên b=5y+4
ab+1
\(=\left(5x+1\right)\left(5y+4\right)+1\)
=25xy+20x+5y+4+1
=25xy+20x+5y+5
=5(5xy+4x+y+1)⋮5
c: \(Q=2n^2\left(n+1\right)-2n\left(n^2+n-3\right)\)
\(=2n^3+2n^2-2n^3-2n^2+6n\)
=6n⋮6
Bài 8:
a: \(A=x^2+2xy-3x^3+2y^3+3x^3-y^3\)
\(=x^2+2xy-3x^3+3x^3+2y^3-y^3\)
\(=x^2+2xy+y^3\)
Khi x=5;y=4 thì \(A=5^2+2\cdot5\cdot4+4^3=25+40+64=129\)
b: x=-1;y=-1
=>xy=1
\(x^2y^2=\left(xy\right)^2=1^2=1;x^4y^4=\left(xy\right)^4=1^4=1\) ; \(x^6y^6=\left(xy\right)^6=1^6=1;x^8y^8=\left(xy\right)^8=1^8=1\)
=>B=1-1+1-1+1=1

Bài 3:
a: Ta có: \(\hat{FAH}+\hat{FAB}+\hat{HAD}+\hat{BAD}=360^0\)
=>\(\hat{FAH}+\hat{DAB}=360^0-90^0-90^0=180^0\)
mà \(\hat{DAB}+\hat{ADC}=180^0\) (ABCD là hình bình hành)
nên \(\hat{FAH}=\hat{CDA}\)
Ta có: ABEF là hình vuông
=>AB=BE=FE=AF
mà AB=CD
nên AB=CD=BE=FE=AF
Ta có: ADGH là hình vuông
=>AD=DG=GH=HA
mà AD=BC
nên BC=AD=DG=GH=HA
Xét ΔFAH và ΔCDA có
FA=CD
\(\hat{FAH}=\hat{CDA}\)
AH=AD
Do đó: ΔFAH=ΔCDA
=>FH=CA
ΔFAH=ΔCDA
=>\(\hat{FHA}=\hat{CAD}\)
Gọi K là giao điểm của AC và FH
Ta có: \(\hat{KAH}+\hat{HAD}+\hat{DAC}=180^0\)
=>\(\hat{KAH}+\hat{DAC}=180^0-90^0=90^0\)
=>\(\hat{KAH}+\hat{FHA}=90^0\)
=>ΔAKH vuông tại K
=>AK⊥FH tại K
=>CA⊥FH tại K
b: Ta có: \(\hat{CDG}=\hat{CDA}+\hat{ADG}=\hat{CDA}+90^0\)
\(\hat{EBC}=\hat{EBA}+\hat{CBA}=90^0+\hat{CBA}\)
mà \(\hat{CDA}=\hat{CBA}\) (ABCD là hình bình hành)
nên \(\hat{CDG}=\hat{EBC}\)
Xét ΔCDG và ΔEBC có
CD=EB
\(\hat{CDG}=\hat{EBC}\)
DG=BC
Do đó: ΔCDG=ΔEBC
=>CG=EC và \(\hat{DCG}=\hat{BEC};\hat{DGC}=\hat{BCE}\)
\(\hat{GCE}=\hat{DCB}-\hat{DCG}-\hat{BCE}\)
\(=\hat{DCB}-\hat{BEC}-\hat{BCE}=180^0-\hat{ADC}-\left(180^0-\hat{EBC}\right)=\hat{EBC}-\hat{ADC}\)
\(=\hat{EBA}+\hat{CBA}-\hat{ADC}=\hat{EBA}=90^0\)
=>ΔGCE vuông cân tại C
Bài 2:
a: BO là phân giác của góc ABD
=>\(\hat{ABO}=\hat{DBO}=\frac12\cdot\hat{ABD}\) (1)
CO là phân giác của góc ACE
=>\(\hat{ACO}=\hat{OCE}=\frac12\cdot\hat{ACE}\left(2\right)\)
Ta có: \(\hat{ABD}+\hat{BAC}=90^0\) (ΔADB vuông tại D)
\(\hat{ACE}+\hat{BAC}=90^0\) (ΔAEC vuông tại E)
Do đó: \(\hat{ABD}=\hat{ACE}\left(3\right)\)
Từ (1),(2) suy ra \(\hat{ABO}=\hat{DBO}=\hat{ACO}=\hat{OCE}\)
Ta có: \(\hat{OBC}+\hat{OCB}\)
\(=\hat{OBD}+\hat{DBC}+\hat{OCE}+\hat{ECB}\)
\(=2\cdot\hat{OBD}+\hat{DBC}+\hat{ECB}=\hat{ABD}+90^0-\hat{ABC}+90^0-\hat{ACB}\)
\(=180^0-\hat{ABC}-\hat{ACB}+\hat{ABD}=\hat{BAC}+\hat{ABD}=90^0\)
=>ΔBOC vuông tại O
b: Xét ΔBMH có
BO là đường cao
BO là đường phân giác
Do đó: ΔBMH cân tại B
mà BO là đường cao
nên O là trung điểm của MH
Xét ΔCNK có
CO là đường cao
CO là đường phân giác
Do đó: ΔCNK cân tại C
mà CO là đường cao
nên O là trung điểm của NK
Xét tứ giác MNHK có
O là trung điểm chung của MH và NK
=>MNHK là hình bình hành
Hình bình hành MNHK có MH⊥NK
nên MNHK là hình thoi
Bài 3:
a: Ta có: \(\hat{F A H} + \hat{F A B} + \hat{H A D} + \hat{B A D} = 36 0^{0}\)
=>\(\hat{F A H} + \hat{D A B} = 36 0^{0} - 9 0^{0} - 9 0^{0} = 18 0^{0}\)
mà \(\hat{D A B} + \hat{A D C} = 18 0^{0}\) (ABCD là hình bình hành)
nên \(\hat{F A H} = \hat{C D A}\)
Ta có: ABEF là hình vuông
=>AB=BE=FE=AF
mà AB=CD
nên AB=CD=BE=FE=AF
Ta có: ADGH là hình vuông
=>AD=DG=GH=HA
mà AD=BC
nên BC=AD=DG=GH=HA
Xét ΔFAH và ΔCDA có
FA=CD
\(\hat{F A H} = \hat{C D A}\)
AH=AD
Do đó: ΔFAH=ΔCDA
=>FH=CA
ΔFAH=ΔCDA
=>\(\hat{F H A} = \hat{C A D}\)
Gọi K là giao điểm của AC và FH
Ta có: \(\hat{K A H} + \hat{H A D} + \hat{D A C} = 18 0^{0}\)
=>\(\hat{K A H} + \hat{D A C} = 18 0^{0} - 9 0^{0} = 9 0^{0}\)
=>\(\hat{K A H} + \hat{F H A} = 9 0^{0}\)
=>ΔAKH vuông tại K
=>AK⊥FH tại K
=>CA⊥FH tại K
b: Ta có: \(\hat{C D G} = \hat{C D A} + \hat{A D G} = \hat{C D A} + 9 0^{0}\)
\(\hat{E B C} = \hat{E B A} + \hat{C B A} = 9 0^{0} + \hat{C B A}\)
mà \(\hat{C D A} = \hat{C B A}\) (ABCD là hình bình hành)
nên \(\hat{C D G} = \hat{E B C}\)
Xét ΔCDG và ΔEBC có
CD=EB
\(\hat{C D G} = \hat{E B C}\)
DG=BC
Do đó: ΔCDG=ΔEBC
=>CG=EC và \(\hat{D C G} = \hat{B E C} ; \hat{D G C} = \hat{B C E}\)
\(\hat{G C E} = \hat{D C B} - \hat{D C G} - \hat{B C E}\)
\(= \hat{D C B} - \hat{B E C} - \hat{B C E} = 18 0^{0} - \hat{A D C} - \left(\right. 18 0^{0} - \hat{E B C} \left.\right) = \hat{E B C} - \hat{A D C}\)
\(= \hat{E B A} + \hat{C B A} - \hat{A D C} = \hat{E B A} = 9 0^{0}\)
=>ΔGCE vuông cân tại C
Bài 2:
a: BO là phân giác của góc ABD
=>\(\hat{A B O} = \hat{D B O} = \frac{1}{2} \cdot \hat{A B D}\) (1)
CO là phân giác của góc ACE
=>\(\hat{A C O} = \hat{O C E} = \frac{1}{2} \cdot \hat{A C E} \left(\right. 2 \left.\right)\)
Ta có: \(\hat{A B D} + \hat{B A C} = 9 0^{0}\) (ΔADB vuông tại D)
\(\hat{A C E} + \hat{B A C} = 9 0^{0}\) (ΔAEC vuông tại E)
Do đó: \(\hat{A B D} = \hat{A C E} \left(\right. 3 \left.\right)\)
Từ (1),(2) suy ra \(\hat{A B O} = \hat{D B O} = \hat{A C O} = \hat{O C E}\)
Ta có: \(\hat{O B C} + \hat{O C B}\)
\(= \hat{O B D} + \hat{D B C} + \hat{O C E} + \hat{E C B}\)
\(= 2 \cdot \hat{O B D} + \hat{D B C} + \hat{E C B} = \hat{A B D} + 9 0^{0} - \hat{A B C} + 9 0^{0} - \hat{A C B}\)
\(= 18 0^{0} - \hat{A B C} - \hat{A C B} + \hat{A B D} = \hat{B A C} + \hat{A B D} = 9 0^{0}\)
=>ΔBOC vuông tại O
b: Xét ΔBMH có
BO là đường cao
BO là đường phân giác
Do đó: ΔBMH cân tại B
mà BO là đường cao
nên O là trung điểm của MH
Xét ΔCNK có
CO là đường cao
CO là đường phân giác
Do đó: ΔCNK cân tại C
mà CO là đường cao
nên O là trung điểm của NK
Xét tứ giác MNHK có
O là trung điểm chung của MH và NK
=>MNHK là hình bình hành
Hình bình hành MNHK có MH⊥NK
nên MNHK là hình thoi


a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)


.png)




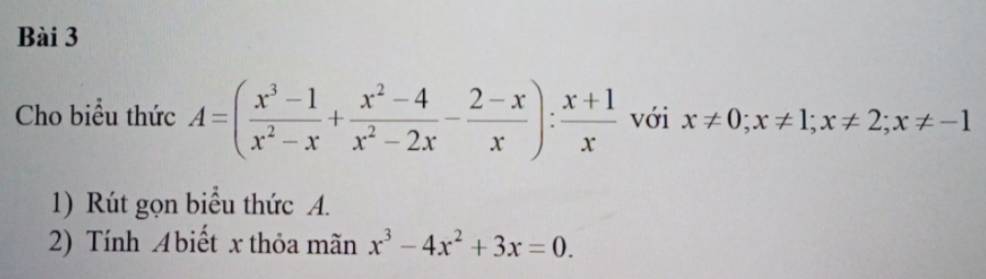

Bài `4`
`1, 2y(x+2)-3x-6`
`=2y(x+2) -(3x+6)`
`=2y(x+2) -3(x+2)`
`=(x+2)(2y-3)`
`2, 3(x+4) -x^2-4x`
`=3(x+4)-(x^2+4x)`
`=3(x+4) -x(x+4)`
`=(x+3)(3-x)`
`3, 2(x+5) -x^2-5x`
`=2(x+5)-(x^2+5x)`
`=2(x+5)-x(x+5)`
`=(x+5)(2-x)`
`4, x^2 +6x-3(x+6)`
`= (x^2+6x) -3(x+6)`
`=x(x+6)-3(x+6)`
`=(x+6)(x-3)`
`5, x(x+y) -5x-5y`
`=x(x+y) -(5x+5y)`
`=x(x+y)-5(x+y)`
`=(x+y)(x-5)`
`6,x(x-y)+2x-2y`
`=x(x-y)+2(x-y)`
`=(x-y)(x+2`
Bạn tách ra từng bài đi ạ. Làm all trong 1 câu nhiều lắm.