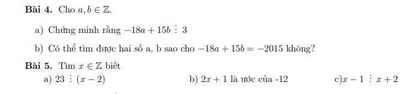Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 4:
a. Ta có: $-18a+15b=3(-6a+5b)\vdots 3$
b. Vì $-18a+15b$ chia hết cho $3$ với $a,b$ nguyên, mà $-2015\not\vdots 3$ nên không tồn tại hai số $a,b$ nguyên thỏa mãn $-18a+15b=-2015$
Bài 5:
a.
$23\vdots x-2$
$\Rightarrow x-2\in$ Ư$(23)$
$\Rightarrow x-2\in\left\{\pm 1;\pm 23\right\}$
$\Rightarrow x\in\left\{3; 1; 25; -21\right\}$
b.
$2x+1\in$ Ư$(-12)$, mà $2x+1$ lẻ nên:
$2x+1\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow x\in\left\{0; -1; 1; -2\right\}$
c.
$x-1\vdots x+2$
$(x+2)-3\vdots x+2$
$3\vdots x+2$
$\Rightarrow x+2\in$ Ư$(3)$
$\Rightarrow x+2\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow x\in\left\{-1; -3; -5; 1\right\}$

Bài 4:
a) \(x+xy-3y=4\)
\(\Leftrightarrow x-3+y\left(x-3\right)=1\)
\(\Leftrightarrow\left(x+y\right)\left(x-3\right)=1\)
mà \(x.y\)là số nguyên nên ta có bảng giá trị:
| x+y | 1 | -1 |
| x-3 | 1 | -1 |
| x | 4 | 2 |
| y | -3 | -3 |
b) \(BCNN\left(6,7\right)=42\)nên \(BC\left(6,7\right)=B\left(42\right)\).
\(200< 6k< 2000\Rightarrow33< k< 334\)
suy ra có \(334-33-1=300\)giá trị của \(x\)là bội của \(6\)mà \(200< x< 2000\).
\(200< 7l< 2000\Rightarrow28< l< 286\)
suy ra có \(286-28-1=257\)giá trị của \(x\)là bội của \(7\)mà \(200< x< 2000\).
\(200< 42m< 2000\Leftrightarrow4< m< 48\)
suy ra có \(48-4-1=43\)giá trị của \(x\)là bội của \(42\)mà \(200< x< 2000\)
Số giá trị của \(x\)thỏa mãn ycbt là: \(300+257-43=514\)(số)

(x - 5) x (x - 7) = 0
=> x - 5 = 0 => x =5
hoặc x - 7 = 0 => x=7
........

1.Chứng minh rằng: \(\frac{12n+1}{30n+2}\)là phân số tối giản.
2.Chứng minh rằng: \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+.....+\frac{1}{100^2}< 1\)
3.Chứng minh rằng nếu ab + cd + eg \(⋮\)11 thì abcdeg \(⋮\)11
4.Chứng minh rằng: 1028 + 8 \(⋮\)72
5.Chứng minh rằng: Cho S = 30 + 32 + 34 + 36 +....+ 32002
a) Tính S
b) Chứng minh S \(⋮\)7
6.Chứng minh rằng: A = 3 + 32 + 33 + 34 +.....+ 3100 \(⋮\)120

\(3\cdot\frac{1}{2}\cdot\frac{1}{4}\)
= \(\frac{3}{1}\cdot\frac{1}{2}\cdot\frac{1}{4}\)
= \(\frac{3}{2}\cdot\frac{1}{4}\)
= \(\frac{3}{8}\)

\(\left(-37\right)+4\left|-6\right|\)
\(=\left(-37\right)+4\cdot6\)
\(=\left(-37\right)+24\)
\(=-13\)
(-37) + 4 . /-6/
= (-37) + 4 . 6
= (-37) + 24
= (-37) - (-24)
= -13
/ là giá trị tuyệt đối nhé

\(\frac{2929-101}{1919+101}=\frac{29\cdot101-101}{19\cdot101+101}=\frac{101\left(29-1\right)}{101\left(19+1\right)}=\frac{14}{5}\)