K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
subjects
CTVHS
18 tháng 8
\(a.\frac12+\frac32x=\frac34\)
\(\frac32x=\frac34-\frac12=\frac14\)
\(x=\frac14:\frac32=\frac14\cdot\frac23=\frac16\)
\(b.2,5-2\cdot\left(x-0,5\right)=2\)
\(2\cdot\left(x-0,5\right)=2,5-2=0,5\)
\(x-0,5=0,5:2=0,25\)
\(x=0,25+0,5=0,75\)
\(c.\left(x+\frac32\right)^3=\frac{125}{8}=\left(\frac52\right)^3\)
\(x+\frac32=\frac52\)
\(x=\frac52-\frac32=\frac22=1\)
\(d.\left(x-\frac13\right)^2=\frac{25}{4}=\left(\pm\frac52\right)^2\)
\(\left[\begin{array}{l}x-\frac13=\frac52\Rightarrow x=\frac{17}{6}\\ x-\frac13=-\frac52\Rightarrow x=-\frac{13}{6}\end{array}\right.\)
vậy \(x\in\left\lbrace\frac{17}{6};-\frac{13}{6}\right\rbrace\)
\(e.7\cdot3^{x-1}-3^{x+2}=-540\)
\(3^{x-1}\cdot\left(7-3^3\right)=-540\)
\(3^{x-1}\cdot\left(7-27\right)=-540\)
\(3^{x-1}\cdot\left(-20\right)=-540\)
\(3^{x-1}=\left(-540\right):\left(-20\right)\)
\(3^{x-1}=27=3^3\)
⇒ x - 1 = 3
⇒ x = 4
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
\(\hat{N_2}\) = \(\hat{N_4}\) (hai góc đối đỉnh)
⇒ \(\hat{M_1}\) = \(\hat{N_4}\) (tính chất bác cầu) (1)
Góc \(\hat{N_1}\) và \(\hat{M_4}\) (hai góc đồng vị) (2)
Từ (1) và (2) ta có:
c // d (đpcm)
19 tháng 8
a: ta có: zz'⊥MN
yy'⊥MN
Do đó: zz'//yy'
=>\(\hat{ABN}=\hat{xAM}\) (hai góc đồng vị)
=>\(\hat{ABN}=70^0\)
b: Ta có: \(\hat{xAM}+\hat{MAB}=180^0\) (hai góc kề bù)
=>\(\hat{MAB}=180^0-70^0=110^0\)
AC là phân giác của góc MAB
=>\(\hat{MAC}=\hat{BAC}=\frac12\cdot\hat{MAB}=\frac12\cdot110^0=55^0\)
Xét ΔACB có \(\hat{ACN}\) là góc ngoài tại đỉnh C
nên \(\hat{ACN}=\hat{CBA}+\hat{CAB}=70^0+55^0=125^0\)
c:
ta có: \(\hat{x^{\prime}BN}+\hat{NBA}=180^0\) (hai góc kề bù)
=>\(\hat{x^{\prime}BN}=180^0-70^0=110^0\)
Bk là phân giác của góc x'BN
=>\(\hat{x^{\prime}Bk}=\hat{NBk}=\hat{x^{\prime}BN}\cdot\frac12=110^0\cdot\frac12=55^0\)
=>\(\hat{x^{\prime}Bk}=\hat{BAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên Bk//AC
S
subjects
CTVHS
18 tháng 8
\(a.\frac47-\frac47:\frac{5}{14}=\frac47-\frac47\cdot\frac{14}{5}\)
\(=\frac47\cdot\left(1-\frac{14}{5}\right)=\frac47\cdot\left(-\frac95\right)=-\frac{36}{35}\)
\(b.\left(-\frac57\right)^2+8\cdot\left(0,5\right)^3+\left(-1\right)^{2025}=\frac{25}{49}+8\cdot0,125-1\)
\(=\frac{25}{49}+1-1=\frac{25}{49}\)
\(c.\left(1-\frac35\right)^2-\left(-\frac34\right)+\left(-\frac{13}{10}\right)=\left(\frac25\right)^2+\frac34-\frac{13}{10}\)
\(=\frac{4}{25}+\frac34-\frac{13}{10}=\frac{16}{100}+\frac{75}{100}-\frac{130}{100}=\frac{16+75-130}{100}=-\frac{39}{100}\)
\(d.\left(-\frac35+\frac49\right):\frac{7}{11}+\left(-\frac25+\frac59\right):\frac{7}{11}=-\frac{7}{45}\cdot\frac{11}{7}+\frac{7}{45}\cdot\frac{11}{7}\)
\(=\frac{11}{7}\cdot\left(\frac{7}{45}-\frac{7}{45}\right)=\frac{11}{7}\cdot0=0\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
Ta có:
\(\hat{Q_3}\) = \(\hat{Q_1}\)(đối đỉnh)
⇒ \(\hat{Q}_1\) = \(\hat{P_1}\) (tính chất bác cầu) (1)
Hai góc \(Q_1\) và \(P_1\) ở vị trí đồng vị (2)
Từ 1 và (2) ta có:
m//n (đpcm)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
Giải:
a; m ⊥ d; n ⊥ d
⇒ m//n (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
b; Điểm B trên hình đâu em?
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 8
Giải:
a; \(\hat{x^{\prime}AB}\) = \(\hat{ABy}\) = 70\(^0\)(gt) (1)
\(\hat{x^{\prime}AB}\) và \(\hat{ABy}\) (hai góc so le trong) (2)
Kết hợp (1) và (2) ta có:
\(xx^{\prime}\) // yy'
b; \(xx^{\prime}\) // yy' (cmt) (a)
mm' ⊥ \(x\)\(x^{\prime}\)(gt) (b)
Từ (a) và (b) ta có:
mm'⊥ yy' (tính chất từ vuông góc đến song song)
⇒ \(\hat{yDm^{\prime}}\) = 90\(^0\)
18 tháng 8
Bài 14:
\(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
\(A\left(x\right)-B\left(x\right)=3x^4+7x^2+8x+2\)
Do đó: \(A\left(x\right)+B\left(x\right)+A\left(x\right)-B\left(x\right)=5x^4-6x^3-3x^2-4+3x^4+7x^2+8x+2\)
=>\(2\cdot A\left(x\right)=8x^4-6x^3+4x^2+8x-2\)
=>\(A\left(x\right)=4x^4-3x^3+2x^2+4x-1\)
Ta có: \(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
=>\(B\left(x\right)=5x^4-6x^3-3x^2-4-4x^4+3x^3-2x^2-4x-1\)
=>\(B\left(x\right)=x^4-3x^3-5x^2-4x-5\)
Bài 13:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=6x^4-3x^2-5+4x^4-6x^3+7x^2+8x-9\)
=>\(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
=>\(g\left(x\right)=6x^4-3x^2-5-5x^4+3x^3-2x^2-4x+7=x^4+3x^3-5x^2-4x+2\)
BM
1
10 tháng 8
Bài 1:
a: \(A\left(x\right)=5x^4-7x^2-3x-6x^2+11x-30\)
\(=5x^4-7x^2-6x^2-3x+11x-30\)
\(=5x^4-13x^2+8x-30\)
\(B=-11x^3+5x-10+5x^4-2+20x^3-34x\)
\(=5x^4+20x^3-11x^3+5x-34x-2-10\)
\(=5x^4+9x^3-29x-12\)
b: A(x)+B(x)
\(=5x^4-13x^2+8x-30+5x^4+9x^3-29x-12\)
\(=10x^4-4x^3-21x-42\)
A(x)-B(x)
\(=5x^4-13x^2+8x-30-5x^4-9x^3+29x+12\)
\(=-9x^3-13x^2+37x-18\)
Bài 2:
a: \(M=2x^2+5x-12\)
Bậc là 2
Hệ số cao nhất là 2
Hệ số tự do là -12
b: M+N
\(=2x^2+5x-12+x^2-8x-1=3x^2-3x-13\)
c: P(2x-3)=M
=>\(P=\frac{2x^2+5x-12}{2x-3}=\frac{2x^2-3x+8x-12}{2x-3}\)
\(=\frac{x\left(2x-3\right)+4\left(2x-3\right)}{2x-3}\)
=x+4
13 tháng 8
a: Ta có: \(\hat{AOD}+\hat{BOD}=180^0\) (hai góc kề bù)
=>\(\hat{BOD}=180^0-97^0=83^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia OA, ta có: \(\hat{AOE}<\hat{AOD}\left(56^0<97^0\right)\)
nên tia OE nằm giữa hai tia OA và OD
=>\(\hat{AOE}+\hat{EOD}=\hat{AOD}\)
=>\(\hat{EOD}=97^0-56^0=41^0\)
Ta có: \(\hat{AOE}+\hat{EOC}+\hat{COB}=180^0\)
=>\(\hat{EOC}=180^0-56^0-42^0=82^0\)
b: Trên cùng một nửa mặt phẳng bờ chứa tia OE, ta có; \(\hat{EOD}<\hat{EOC}\left(41^0<82^0\right)\)
nên tia OD nằm giữa hai tia OE và OC
=>\(\hat{EOD}+\hat{DOC}=\hat{EOC}\)
=>\(\hat{DOC}=82^0-41^0=41^0\)
Ta có: tia OD nằm giữa hai tia OE và OC
\(\hat{DOE}=\hat{DOC}\left(=41^0\right)\)
Do đó: OD là phân giác của góc EOC
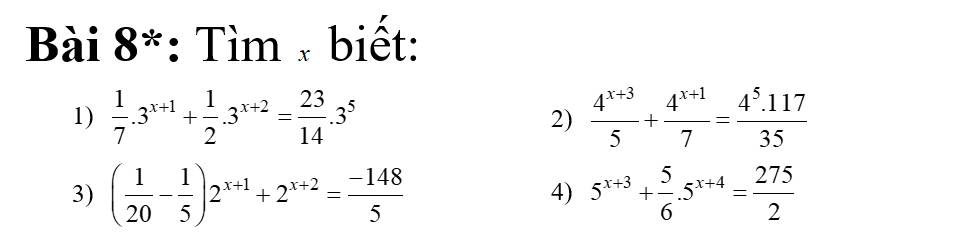
1: \(\Leftrightarrow3^x\cdot\dfrac{1}{7}\cdot3+3^x\cdot9\cdot\dfrac{1}{2}=\dfrac{23}{14}\cdot3^5\)
=>\(3^x\left(\dfrac{3}{7}+\dfrac{9}{2}\right)=\dfrac{23}{14}\cdot3^5\)
=>\(3^x\cdot\dfrac{69}{14}=\dfrac{23}{14}\cdot3^5\)
=>\(3^{x+1}\cdot\dfrac{23}{14}=\dfrac{23}{14}\cdot3^5\)
=>\(3^{x+1}=3^5\)
=>x+1=5
=>x=4
2: \(\Leftrightarrow4^x\cdot\dfrac{64}{5}+4^x\cdot\dfrac{4}{7}=4^5\cdot\dfrac{117}{35}\)
=>\(4^x\left(\dfrac{64}{5}+\dfrac{4}{7}\right)=4^5\cdot\dfrac{117}{35}\)
=>\(4^{x+1}\cdot\left(\dfrac{16}{5}+\dfrac{1}{7}\right)=4^5\cdot\dfrac{117}{35}\)
=>\(4^{x+1}=4^5\)
=>x+1=5
=>x=4
3:
\(\Leftrightarrow2^x\cdot2\cdot\dfrac{-3}{20}+2^x\cdot4=-\dfrac{148}{5}\)
=>\(2^x\cdot\left(-\dfrac{3}{10}+4\right)=-\dfrac{148}{5}\)
=>\(2^x=-8\)
=>\(x\in\varnothing\)
4: \(\Leftrightarrow5^x\cdot125+\dfrac{5}{6}\cdot5^x\cdot625=\dfrac{275}{2}\)
=>\(5^x\left(125+625\cdot\dfrac{5}{6}\right)=\dfrac{275}{2}\)
=>\(5^x=\dfrac{33}{155}\)
=>\(x\in\varnothing\)
cảm ơn bạn nha