
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(4\left(xy\right)^2\cdot x=4x^2y^2\cdot x=4x^3y^2\)
Nhóm 1: \(x^3y;-7x^3y\)
Nhóm 2: \(x^2y;3x^2y\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{b-a}{5-3}=\dfrac{-16}{2}=-8\)
Do đó: a=-24; b=-40

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\) (*)
a) Từ (*) ta có:
\(\dfrac{5a+3b}{5a-3b}=\dfrac{5bk+3b}{5bk-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\) (1)
\(\dfrac{5c+3d}{5c-3d}=\dfrac{5dk+3d}{5dk-3d}=\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\) (2)
Từ (1) và (2) suy ra \(\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)
b) Từ (*) ta có:
\(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7b^2k^2+3b^2k}{11b^2k^2-8b^2}=\dfrac{b^2\left(7k^2+3k\right)}{b^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\) (3)
\(\dfrac{7c^2+3cd}{11c^2-8d^2}=\dfrac{7d^2k^2+3d^2k}{11d^2k^2-8d^2}=\dfrac{d^2\left(7k^2+3k\right)}{d^2\left(11k^2-8\right)}=\dfrac{7k^2+3k}{11k^2-8}\) (4)
Từ (3) và (4) suy ra \(\dfrac{7a^2+3ab}{11a^2-8b^2}=\dfrac{7c^2+3cd}{11c^2-8d^2}\)
P/s: test lại đề phần b), mẫu số của vế trái
a, Ta có : \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Vì \(\dfrac{a}{c}=\dfrac{b}{d}\Rightarrow\dfrac{5a}{5c}=\dfrac{3b}{3d}\)\(=\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
\(\Rightarrow\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\left(đpcm\right)\)
Vậy \(\dfrac{5a+3b}{5a-3b}=\dfrac{5c+5d}{5c-5d}\)

\(\frac{13}{38}>\frac{13}{39}\) => \(\frac{13}{38}>\frac{1}{3}\)
\(\frac{12}{37}<\frac{12}{36}\) => \(\frac{12}{37}<\frac{1}{3}\)
=> 13/38 > 12/37


a, \(\frac{3}{4}-x=\frac{1}{2}\Leftrightarrow x=\frac{3}{4}-\frac{1}{2}=\frac{1}{4}\)Vậy \(x=\frac{1}{4}\)
b, \(\left|x+\frac{2}{3}\right|=\frac{5}{6}\)
TH1 : \(x+\frac{2}{3}=\frac{5}{6}\Leftrightarrow x=\frac{5}{6}-\frac{2}{3}=\frac{1}{6}\)
TH2 : \(x+\frac{2}{3}=-\frac{5}{6}\Leftrightarrow x=-\frac{5}{6}-\frac{2}{3}=\frac{-9}{6}=\frac{-3}{2}\)
Vậy \(x=\left\{\frac{1}{6};-\frac{3}{2}\right\}\)
a,\(\frac{3}{4}-x=\frac{1}{2}\)
\(\Leftrightarrow x=\frac{3}{4}-\frac{1}{2}\)
\(\Leftrightarrow x=\frac{1}{4}\)
b,\(\left|x+\frac{2}{3}\right|=\frac{5}{6}\)
\(\Leftrightarrow x+\frac{2}{3}=\pm\frac{5}{6}\)
TH1:\(x+\frac{2}{3}=\frac{5}{6}\)
\(\Leftrightarrow x=\frac{5}{6}-\frac{2}{3}\)
\(\Leftrightarrow x=\frac{1}{6}\)
TH2:\(x+\frac{2}{3}=-\frac{5}{6}\)
\(\Leftrightarrow x=-\frac{5}{6}-\frac{2}{3}\)
\(\Leftrightarrow x=-\frac{3}{2}\)

TH1: x>=17
=>4x-68>=0
=>|4x-68|=4x-68
=>E=-(4x-68)+4x+99=-4x+68+4x+99=167
=>GTLN của E là E=167 khi x>=17(1)
TH2: x<17
=>4x-68<0
=>|4x-68|=-4x+68
=>E=-(-4x+68)+4x+99=4x-68+4x+99=8x+31
Vì hàm số E=8x+31 là hàm số đồng biến trên R
nên E lớn nhất khi x lớn nhất
Khi x<17 thì x không có giá trị lớn nhất
=>E không có giá trị lớn nhất khi x<17(2)
Từ (1),(2) suy ra \(E_{\max}=167\) khi x>=17
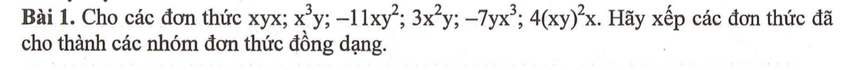 giúp mềnh với ạ=(((
giúp mềnh với ạ=((( giúp mềnh với ạ
giúp mềnh với ạ
lỗi
giúp j bạn