
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


câu 1:
a2+b2+c2+42 = 2a+8b+10c
<=> a2-2a+1+b2 -8b+16+c2-10c+25=0
<=> (a-1)2+(b-4)2+(c-5)2=0
<=>a=1 và b=4 và c=5
=> a+b+c = 10
ta có 2(a2+b2)=5ab
<=> 2a2+2b2-5ab=0
<=> 2a2-4ab-ab+2b2=0
<=> 2a(a-2b)-b(a-2b)=0
<=> (a-2b)(2a-b)=0
<=> a=2b(thỏa mãn)
hoặc b=2a( loại vì a>b)
với a=2b =>P=5b/5b=1

câu 14 : chọn đáp án \(B\) vì \(\left|\overrightarrow{b}\right|=\sqrt{\left(1\right)^2+\left(-1\right)^2}=\sqrt{2}\ne0\)
câu 18 : ta có tọa độ trọng tâm \(G\) của tam giác \(ABC\)
là \(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}\\y_G=\dfrac{y_A+y_B+y_C}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_G=\dfrac{2+3-7}{3}\\y_G=\dfrac{1-1+3}{3}\end{matrix}\right.\) \(\left\{{}\begin{matrix}x_G=\dfrac{-2}{3}\\y_G=1\end{matrix}\right.\)
vậy tọa độ trọng tâm \(G\) là \(G\left(\dfrac{-2}{3};1\right)\) \(\Rightarrow\) chọn đáp án \(B\)
câu 19 : đặt tọa độ của điểm \(D\) là \(D\left(x_D;y_D\right)\)
\(\Rightarrow\) \(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(1;-7\right)\\\overrightarrow{DC}=\left(4-x_D;3-y_D\right)\end{matrix}\right.\)
ta có \(ABCD\) là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\Leftrightarrow\left\{{}\begin{matrix}1=4-x_D\\-7=3-y_D\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_D=3\\y_D=10\end{matrix}\right.\)
vậy tọa độ điểm \(D\) là \(D\left(3;10\right)\) \(\Rightarrow\) chọn đáp án \(A\)

Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
DO đó; OM là tia phân giác của góc AOB
Xét ΔOAM vuông tại A có
\(\tan\widehat{AOM}=\dfrac{AM}{AO}=\sqrt{3}\)
nên \(\widehat{AOM}=60^0\)
=>\(\widehat{AOB}=120^0\)

Oh, giống tôi quá, bạn cũng thích sưu tầm danh ngôn tâm trạng à ?

Ta thừa nhận định lý f(x) chia hết cho x-a thì f(a) =0 ( mình đang vội khỏi chứng minh nhé, nếu thắc mắc phiền bạn xem SGK 9 nha)
Thay 1 vào x, ta có
f(x) =14+12+a=0
2+a=0 suy ra a=-2


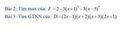

























 Giari hộ mình câu này với, mình cần gấp.
Giari hộ mình câu này với, mình cần gấp.







Bài 2.
\(F=2-3\left[\left(x+1\right)^4+\left(x-5\right)^4\right]\)
Ta có bất đẳng thức phụ:
\(a^4+b^4\ge\frac{1}{8}\left(a+b\right)^4\)
Chứng minh:
\(8\left(a^4+b^4\right)\ge4\left(a^2+b^2\right)^2=\left[2\left(a^2+b^2\right)\right]^2\ge\left(a+b\right)^4\)
(vì \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\))
Dấu \(=\)khi \(a=b\).
Áp dụng ta có:
\(\left(x+1\right)^4+\left(5-x\right)^4\ge\frac{1}{8}\left(x+1+5-x\right)^4=\frac{1}{8}.6^4=162\).
\(F\le2-3.162=-484\)
Dấu \(=\)khi \(x+1=5-x\Leftrightarrow x=2\).
Bài 3.
\(D=\left(2x-1\right)\left(x+2\right)\left(x+3\right)\left(2x+1\right)\)
\(=\left[\left(2x-1\right)\left(x+3\right)\right]\left[\left(x+2\right)\left(2x+1\right)\right]\)
\(=\left(2x^2+5x-3\right)\left(2x^2+5x+2\right)\)
\(=\left(2x^2+5x-\frac{1}{2}\right)^2-\left(\frac{5}{2}\right)^2\ge-\left(\frac{5}{2}\right)^2=-\frac{25}{4}\)
Dấu \(=\)khi \(2x^2+5x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{4}\left(-5\pm\sqrt{29}\right)\).