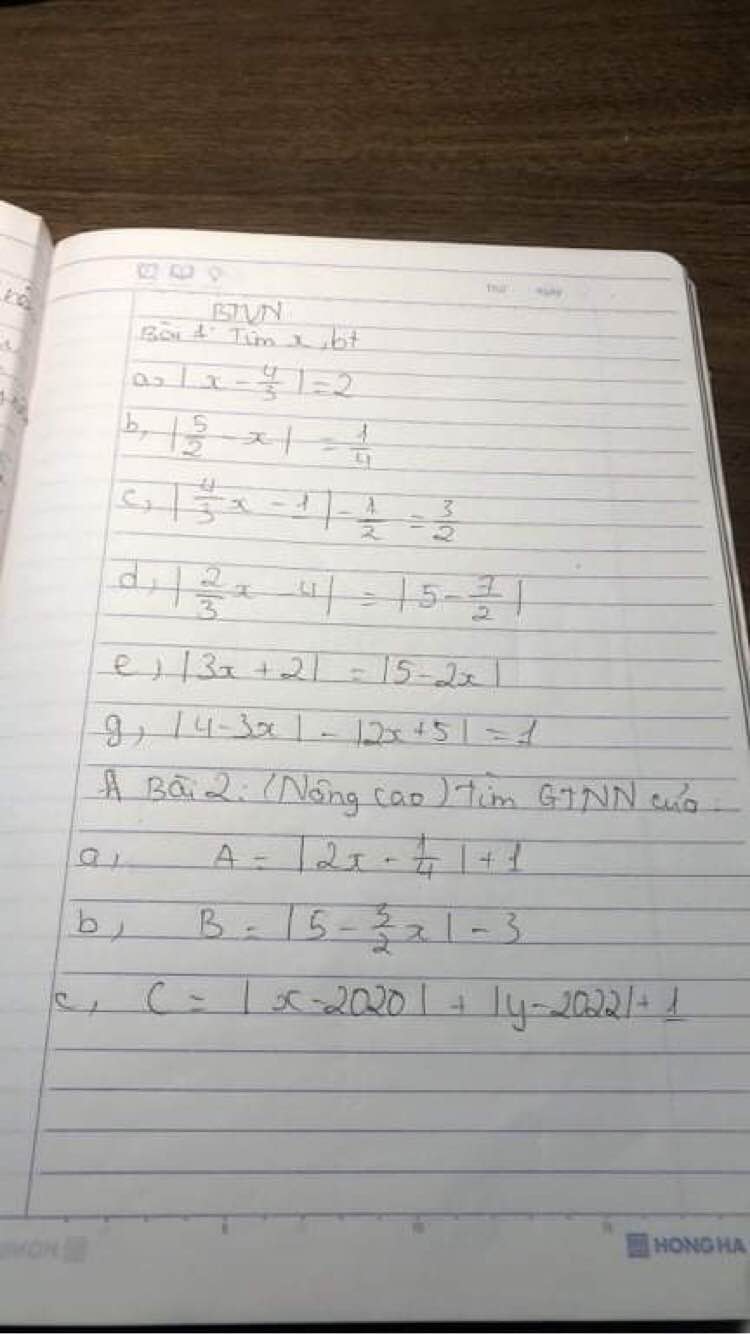Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a. $x^2=12y^2+1$ lẻ nên $x$ lẻ
Ta biết một scp khi chia 8 dư $0,1,4$. Mà $x$ lẻ nên $x^2$ chia $8$ dư $1$
$\Rightarrow 12y^2+1\equiv 1\pmod 8$
$\Rightarrow 12y^2\equiv 0\pmod 8$
$\Rightarrow y^2\equiv 0\pmod 2$
$\Rightarrow y$ chẵn. Mà $y$ nguyên tố nên $y=2$.
Khi đó: $x^2=12y^2+1=12.2^2+1=49\Rightarrow x=7$ (tm)
Bài 2:
b.
$x^2=8y+1$ nên $x$ lẻ. Đặt $x=2k+1$ với $k$ tự nhiên.
Khi đó: $8y+1=x^2=(2k+1)^2=4k^2+4k+1$
$\Rightarrow 2y=k(k+1)$
Vì $(k,k+1)=1, k< k+1$ và $y$ nguyên tố nên xảy ra các TH sau:
TH1: $k=2, k+1=y\Rightarrow y=3\Rightarrow x=5$ (tm)
TH2: $k=1, k+1=2y\Rightarrow y=1$ (vô lý)
TH3: $k=y, k+1=2\Rightarrow y=1$ (vô lý)
Vậy $(x,y)=(5,3)$ là đáp án duy nhất thỏa mãn.

Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5

62/
Đặt \(\frac{x}{2}=\frac{y}{5}=k \)
Suy ra : x = 2k ; y = 5k
Từ x . y = 10 suy ra 2k . 5k = 10k2 = 10 => k2 = 1 => k = ±1
Với k = 1 ta có :
2 . 1 = 2 ; 5 . 1 = 5
Với k = -1 ta có :
2. (-1) = -2 ; 5 . (-1) = -5
Vậy x = ±2 và y = ±5
63/
Theo bài ra ta có :
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\)
Suy ra:
\(\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
Đây là 2 bài trong SGK nhé bạn

Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a-b}{4-3}=2\)
Do đó: a=8; b=6; c=4

Bài 1:
Gọi hai số cần tìm là \(a,b\).
Hai số lần lượt tỉ lệ với \(4,7\)nên \(\frac{a}{4}=\frac{b}{7}\).
Đặt \(\frac{a}{4}=\frac{b}{7}=t\Leftrightarrow\hept{\begin{cases}a=4t\\b=7t\end{cases}}\)
\(ab=4t.7t=28t^2=112\Leftrightarrow t^2=4\Leftrightarrow\orbr{\begin{cases}t=2\\t=-2\end{cases}}\)
Với \(t=2\Rightarrow\hept{\begin{cases}a=2.4=8\\b=2.7=14\end{cases}}\)
Với \(t=-2\Rightarrow\hept{\begin{cases}a=-2.4=-8\\b=-2.7=-14\end{cases}}\).
Bài 2:
Gọi hai số cần tìm là \(a,b\).
Hai số lần lượt tỉ lệ với \(3,4\)nên \(\frac{a}{3}=\frac{b}{4}\).
Đặt \(\frac{a}{3}=\frac{b}{4}=t\Leftrightarrow\hept{\begin{cases}a=3t\\b=4t\end{cases}}\)
\(ab=3t.4t=12t^2=48\Leftrightarrow t^2=4\Leftrightarrow\orbr{\begin{cases}t=2\\t=-2\end{cases}}\)
Với \(t=2\Rightarrow\hept{\begin{cases}a=2.3=6\\b=2.4=8\end{cases}}\)
Với \(t=-2\Rightarrow\hept{\begin{cases}a=-2.3=-6\\b=-2.4=-8\end{cases}}\).

6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2

Bài 2:
a, A= | 2x - \(\dfrac{1}{4}\) | + 1
Ta có | 2x - \(\dfrac{1}{4}\) | ≥ 0 (∀x ∈ R)
⇒| 2x - \(\dfrac{1}{4}\) | + 1 ≥ 1
⇒ GTNN của A là 1
b, B= | 5 - \(\dfrac{3}{2}\)x | - 3
Ta có | 5 - \(\dfrac{3}{2}\)x | ≥ 0 (∀x ∈ R)
⇒ | 5 - \(\dfrac{3}{2}\)x | - 3 ≥ -3
⇒ GTNN của B là -3
c, C= |x - 2020| + |y - 2022| + 1
Ta có |x - 2020| ≥ 0 (∀x ∈ R)
|y - 2022| ≥ 0 (∀y ∈ R)
⇒|x - 2020| + |y - 2022| ≥ 0 (∀x,y ∈ R)
⇒|x - 2020| + |y - 2022| + 1 ≥ 1
⇒ GTNN của C là 1

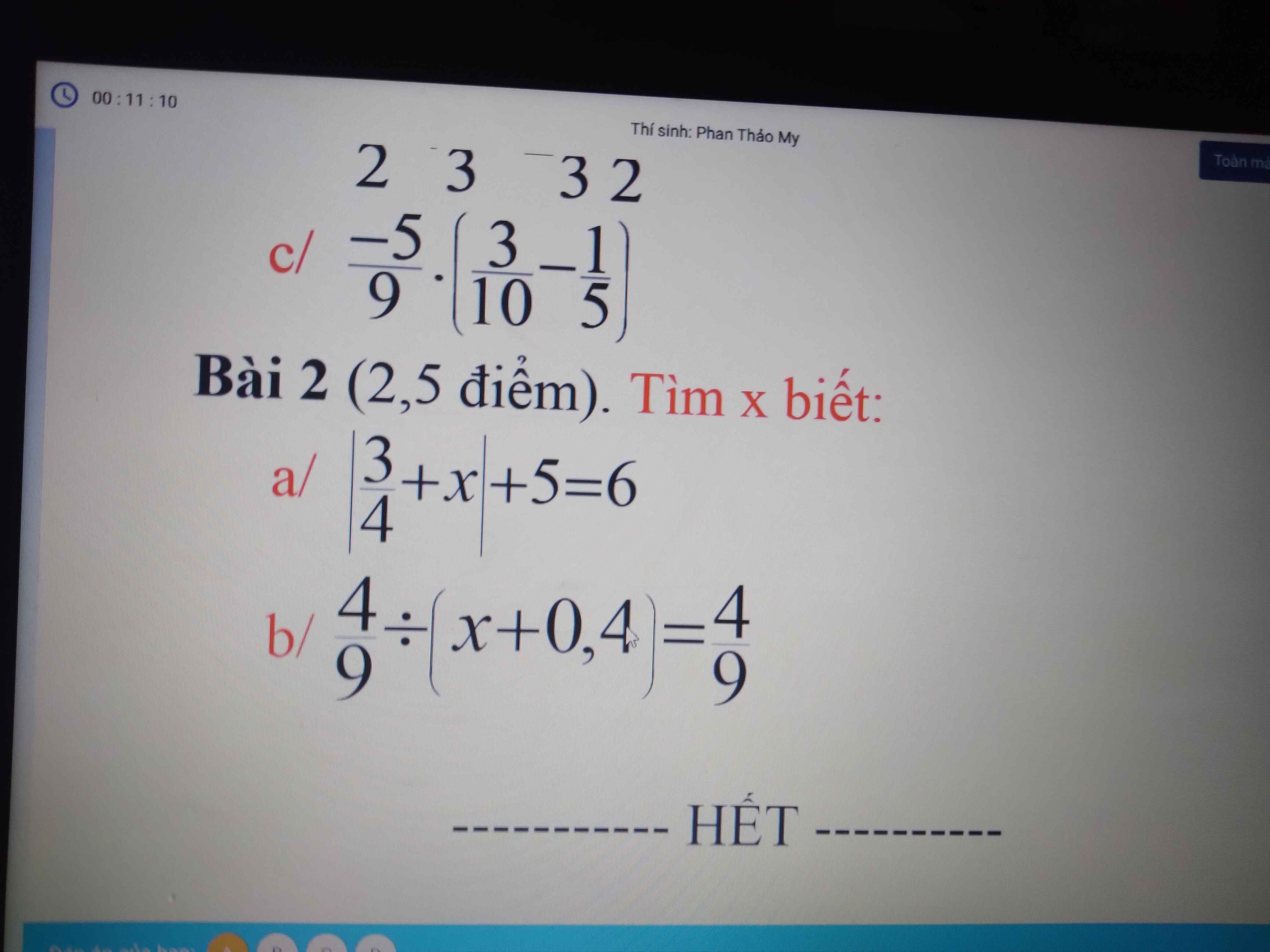
Bài 2:
\(a,\Rightarrow\left|\dfrac{3}{4}+x\right|=1\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{4}+x=1\\\dfrac{3}{4}+x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=-\dfrac{7}{4}\end{matrix}\right.\\ b,\Leftrightarrow x+\dfrac{2}{5}=\dfrac{4}{9}:\dfrac{4}{9}=1\Leftrightarrow x=\dfrac{3}{5}\)
b: \(\dfrac{4}{9}:\left(x+\dfrac{2}{5}\right)=\dfrac{4}{9}\)
\(\Leftrightarrow x+\dfrac{2}{5}=1\)
hay \(x=\dfrac{3}{5}\)

Bài 2:
a,gọi các góc a,b,c,d của tứ giác abcd lần lượt là a,b,c,d(a,b,c,d thuộc n,a,b,c,d<360)
=>a/1=b/2=c/3=d/4
Ta có Góc a+b+c+d=360(tổng các góc của 1 tứ giác)=>áp dung tính chất dãy tỉ số bằng nhau ta có a/1=b/2=c/3=d/4=>a+b+c+d/1+2+3+4=360/10=36
=>a=36,b=72,c=108,d=144
b,
b, Có ˆAA^+ˆDD^=36o36o+144o144o
=180o180o
mà 2 góc này ở vị trí slt
=>AB//CD
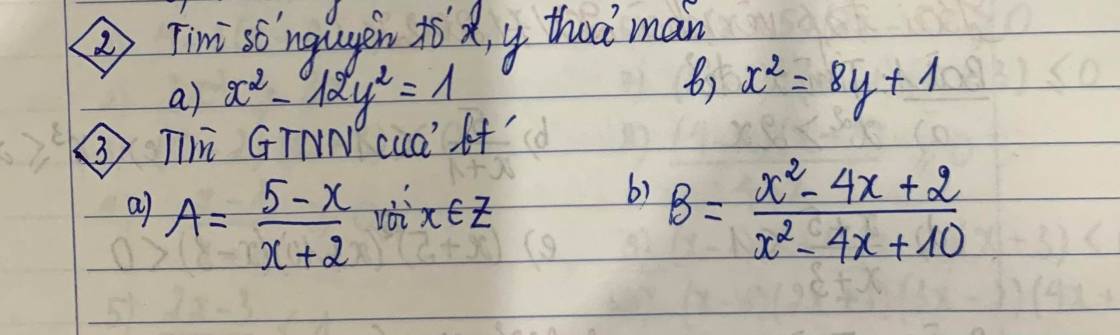
 MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ 2 với ạ
2 với ạ giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ