LT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
3
18 tháng 4 2017
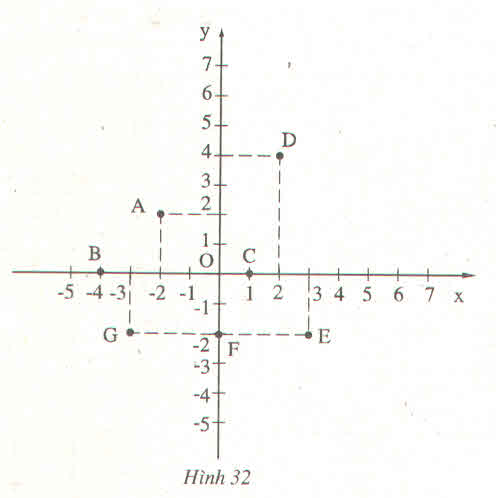
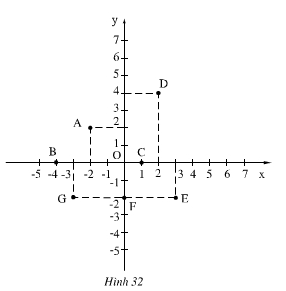
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)
6 tháng 9
d: \(\left(-\frac34+\frac25\right):\frac37+\left(\frac35-\frac14\right):\frac37\)
\(=\left(-\frac34+\frac25+\frac35-\frac14\right):\frac37\)
\(=\left(1-1\right):\frac37=0\)
e: \(\frac59:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac59:\left(\frac{1}{15}-\frac23\right)\)
\(=\frac59:\left(\frac{2}{22}-\frac{5}{22}\right)+\frac59:\left(\frac{1}{15}-\frac{10}{15}\right)\)
\(=\frac59:\frac{-3}{22}+\frac59:\frac{-9}{15}\)
\(=\frac59\cdot\frac{-22}{3}+\frac59\cdot\frac{-5}{3}=\frac59\left(-\frac{22}{3}-\frac53\right)=\frac59\cdot\frac{-27}{3}=-5\)
6 tháng 9
a: \(\left(-\frac54x+3,25\right)\left\lbrack\frac35-\left(-\frac52x\right)\right\rbrack=0\)
=>\(\left(\frac54x-\frac{13}{4}\right)\left(\frac52x+\frac35\right)=0\)
=>\(\left[\begin{array}{l}\frac54x-\frac{13}{4}=0\\ \frac52x+\frac35=0\end{array}\right.\Rightarrow\left[\begin{array}{l}\frac54x=\frac{13}{4}\\ \frac52x=-\frac35\end{array}\right.\Rightarrow\left[\begin{array}{l}x=\frac{13}{4}:\frac54=\frac{13}{5}\\ x=-\frac35:\frac52=-\frac{6}{25}\end{array}\right.\)
b: \(\left(-\frac72x+1,75\right)\left\lbrack\frac45-\left(-\frac53x\right)\right\rbrack=0\)
=>\(\left[\begin{array}{l}-\frac72x+1,75=0\\ \frac45-\left(-\frac53x\right)=0\end{array}\right.\Longrightarrow\left[\begin{array}{l}-\frac72x=-1,75=-\frac74\\ \frac53x=-\frac45\end{array}\right.\)
=>\(\left[\begin{array}{l}x=\frac{-7}{4}:\frac{-7}{2}=\frac24=\frac12\\ x=-\frac45:\frac53=-\frac45\cdot\frac35=-\frac{12}{25}\end{array}\right.\)
c: \(\left(x^2-4\right)\left(x+\frac27\right)=0\)
=>\(\left[\begin{array}{l}x^2-4=0\\ x+\frac27=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x^2=4\\ x=-\frac27\end{array}\right.\Rightarrow\left[\begin{array}{l}x=2\\ x=-2\\ x=-\frac27\end{array}\right.\)
d: \(\left(25-x^2\right)\left(5x-\frac59\right)=0\)
=>\(\left[\begin{array}{l}25-x^2=0\\ 5x-\frac59=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x^2=25\\ 5x=\frac59\end{array}\right.\Rightarrow\left[\begin{array}{l}x=5\\ x=-5\\ x=\frac19\end{array}\right.\)
Thông cảm mk bị cận!
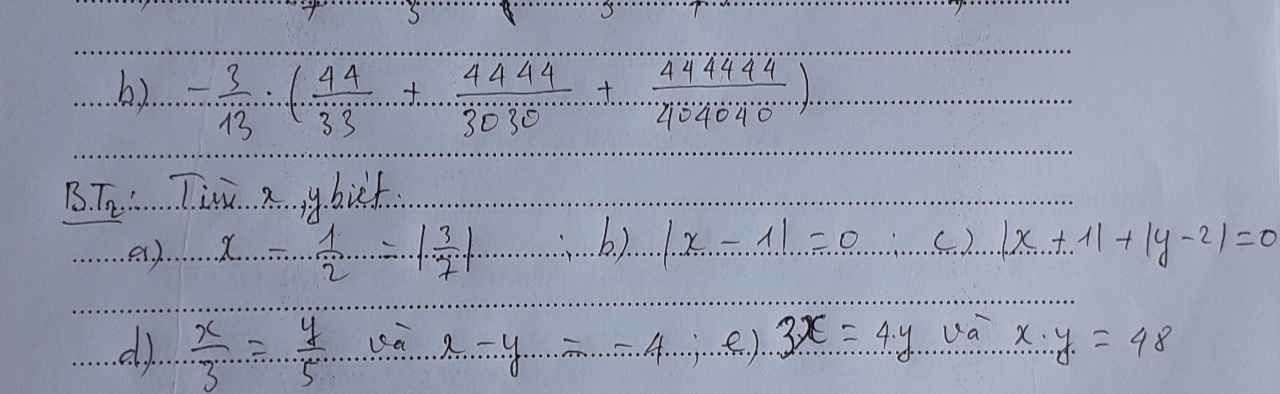
a) Ta có: \(x-\dfrac{1}{2}=\left|\dfrac{3}{7}\right|\)
nên \(x-\dfrac{1}{2}=\dfrac{3}{7}\)
hay \(x=\dfrac{3}{7}+\dfrac{1}{2}=\dfrac{6}{14}+\dfrac{7}{14}=\dfrac{13}{14}\)
b) Ta có: |x-1|=0
nên x-1=0
hay x=1
c) Ta có: \(\left|x+1\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
d) Ta có: \(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x-y=-4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{-4}{-2}=2\)
Do đó: x=6; y=10
e) Ta có: 3x=4y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}\)
Đặt \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k\\y=\dfrac{1}{4}k\end{matrix}\right.\)
Ta có: xy=48
nên \(\dfrac{1}{3}k\cdot\dfrac{1}{4}k=48\)
\(\Leftrightarrow k^2\cdot\dfrac{1}{12}=48\)
\(\Leftrightarrow k^2=48\cdot12=576\)
hay \(k\in\left\{24;-24\right\}\)
Trường hợp 1: k=24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot24=8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot24=6\end{matrix}\right.\)
Trường hợp 2: k=-24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot\left(-24\right)=-8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot\left(-24\right)=-6\end{matrix}\right.\)