
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

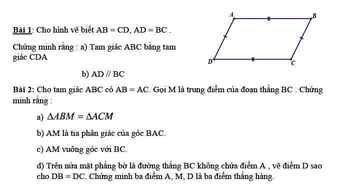
Bài 1:
a, Xét ΔABC và ΔCDA có:
AB=CD(gt)
AD=BC(gt)
Chung AC
⇒ΔABC = ΔCDA (c.c.c)
b, ΔABC = ΔCDA(cma) ⇒\(\widehat{ACB}=\widehat{CAD}\) ( 2 góc tương ứng)
Mà 2 góc này ở vị trị so le trong với nhau ⇒ AD // BC
Bn vẽ hình bài 1 cho mik đc ko ạ! Mik chưa hiểu rõ lắm!

Câu 11: C
Câu 13: B
Câu 14: B
Câu 15: D
Câu 16: C
Câu 17: D
Câu 18: C
Câu 19: A
Câu 20: B

Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
d: \(AH^2-AN^2=HN^2\)
\(BH^2-BM^2=MH^2\)
mà HN=MH
nên \(AH^2-AN^2=BH^2-BM^2\)
hay \(AH^2+BM^2=BH^2+AN^2\)

a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH

b: Xét tứ giác AMNC có
B là trung điểm của AN
B là trung điểm của MC
Do đó: AMNC là hình bình hành
Suy ra: AM//CN

b: \(\widehat{ACB}+\widehat{B}=90^0\)
\(\widehat{HAB}+\widehat{B}=90^0\)
Do đó: \(\widehat{ACB}=\widehat{HAB}\)











Trả lời:
Bài II :
a, \(\frac{3}{8}+\frac{1}{8}:x=\frac{3}{16}\)
\(\Leftrightarrow\frac{1}{8}:x=\frac{3}{16}-\frac{3}{8}\)
\(\Leftrightarrow\frac{1}{8}:x=-\frac{3}{16}\)
\(\Leftrightarrow x=\frac{1}{8}:\left(-\frac{3}{16}\right)\)
\(\Leftrightarrow x=-\frac{2}{3}\)
b, \(\left|2x+1\right|+\frac{3}{2}=3\)
\(\Leftrightarrow\left|2x+1\right|=\frac{3}{2}\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=\frac{3}{2}\\2x+1=-\frac{3}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=\frac{1}{2}\\2x=-\frac{5}{2}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{1}{4}\\x=-\frac{5}{4}\end{cases}}}\)
c, \(\frac{1}{4}x^2-3x=0\)
\(\Leftrightarrow x\left(\frac{1}{4}x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\\frac{1}{4}x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=12\end{cases}}}\)
d, \(7^{x+2}+2.7^x=357\)
\(\Leftrightarrow7^x.7^2+2.7^x=357\)
\(\Leftrightarrow7^x\left(7^2+2\right)=357\)
\(\Leftrightarrow7^x.51=357\)
\(\Leftrightarrow7^x=7\)
\(\Leftrightarrow7^x=7^1\)
\(\Leftrightarrow x=1\)
Bài III :
a, \(\frac{x}{8}=\frac{1}{5}\)
\(\Leftrightarrow x=\frac{1}{5}.8=\frac{8}{5}\)
b, \(2x:8=0,3:0,6\)
\(\Leftrightarrow2x:8=0,5\)
\(\Leftrightarrow2x=0,5.8\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\)
c, \(\frac{2x-1}{4}=\frac{3}{5}\)
\(\Leftrightarrow5\left(2x-1\right)=12\)
\(\Leftrightarrow10x-5=12\)
\(\Leftrightarrow10x=17\)
\(\Leftrightarrow x=\frac{17}{10}\)
d, \(\frac{x-1}{3}=\frac{x+2}{5}\)
\(\Leftrightarrow5\left(x-1\right)=3\left(x+2\right)\)
\(\Leftrightarrow5x-5=3x+6\)
\(\Leftrightarrow5x-3x=6+5\)
\(\Leftrightarrow2x=11\)
\(\Leftrightarrow x=\frac{11}{2}\)
Bài IV :
a, \(A=-\left(\frac{1}{2}x-1\right)^2-\left(x^2-4\right)^4+2021\)
Ta có: \(-\left(\frac{1}{2}x-1\right)^2\le0\forall x;-\left(x^2-4\right)^4\le0\forall x\)
\(\Leftrightarrow-\left(\frac{1}{2}x-1\right)^2-\left(x^2-4\right)^4\le0\forall x\)
\(\Leftrightarrow-\left(\frac{1}{2}x-1\right)^2-\left(x^2-4\right)^4+2021\le2021\forall x\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\frac{1}{2}x-1=0\\x^2-4=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\x=\pm2\end{cases}\Rightarrow x=2}}\)
Vậy GTLN của A = 2021 khi x = 2
b, Ta có : \(\left(2x-3y\right)^2+\left|7y-5z\right|=0\)
Mà \(\left(2x-3y\right)^2\ge0\forall x,y;\left|7y-5z\right|\ge0\forall y,z\)
\(\Rightarrow\hept{\begin{cases}2x-3y=0\\7y-5z=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x=3y\\7y=5z\end{cases}\Leftrightarrow}\hept{\begin{cases}\frac{x}{3}=\frac{y}{2}\\\frac{y}{5}=\frac{z}{7}\end{cases}\Leftrightarrow}\hept{\begin{cases}\frac{x}{15}=\frac{y}{10}\left(1\right)\\\frac{y}{10}=\frac{z}{14}\left(2\right)\end{cases}}}\)
Từ (1) và (2) => \(\frac{x}{15}=\frac{y}{10}=\frac{z}{14}\)
Đặt \(\frac{x}{15}=\frac{y}{10}=\frac{z}{14}=k\left(k\ne0\right)\)
\(\Rightarrow\hept{\begin{cases}x=15k\\y=10k\\z=14k\end{cases}\Rightarrow\hept{\begin{cases}x^2=225k^2\\y^2=100k^2\\z=196k^2\end{cases}}}\)
Ta có : x2 + y2 + z2 = 1024
=> 225k2 + 100k2 + 196k2 = 1024
<=> 521k2 = 1024
=> k2 = \(\frac{1024}{521}\)
=> k = \(\pm\sqrt{\frac{1024}{521}}\)
\(\Rightarrow\hept{\begin{cases}x=15k=15\sqrt{\frac{1024}{521}}\\y=10k=10\sqrt{\frac{1024}{521}}\\z=14k=14\sqrt{\frac{1024}{521}}\end{cases}}\) hoặc \(\hept{\begin{cases}x=15k=15.\left(-\sqrt{\frac{1024}{521}}\right)=-15\sqrt{\frac{1024}{521}}\\y=10k=10.\left(-\sqrt{\frac{1024}{521}}\right)=-10\sqrt{\frac{1024}{521}}\\z=14.\left(-\sqrt{\frac{1024}{521}}\right)=-14\sqrt{\frac{1024}{521}}\end{cases}}\)
mấy câu dễ này chịu khó làm đi b