NN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VK
0
CM
30 tháng 10 2019
Đáp án D.
Ta dễ thấy hai đường thẳng d và d ' song song.
Hai đường thẳng d và d ' lần lượt đi qua hai điểm M 5 ; 1 ; 5 và N 3 ; − 3 ; 1 và có vtcp u → = 2 ; − 1 ; 1 . Ta có M N → = − 2 ; − 4 ; − 4 .
Hai vecto M N → và u → không cùng phương và có giá nằm trên mặt phẳng P nên ta có vtpt của mặt phẳng P là n → = M N → ; u → .
Ta tìm tọa độ của n → bằng MTCT:
⇒ n → = − 8 ; − 6 ; 10
Mặt phẳng P có vtpt n → = − 8 ; − 6 ; 10 và đi qua M 5 ; 1 ; 5 nên có phương trình P : − 8 x − 5 − 6 y − 1 + 10 z − 5 = 0 ⇔ P : 4 x + 3 y − 5 z + 2 = 0 .Ta chọn D.
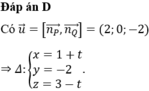
từ phương trình thứ nhất ta có y = 1 + x
từ phương trình thứ 3 ta có z = 8 - x
Thay vào phương trình 2 có 1 + x - (8-x) = -1 <=> 2x = 6 <=> x = 3
Từ đó thay lại vào pt 1 và 3 tính ra
y = 4
z = 5
Bạn viết đầy đủ ra như thế này
từ phương trình thứ nhất ta có y = 1 + x
từ phương trình thứ 3 ta có z = 8 - x
Thay vào phương trình 2 có 1 + x - (8-x) = -1 <=> 2x = 6 <=> x = 3
Từ đó thay lại vào pt 1 và 3 tính ra
y = 4
z = 5