Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
3. Giải thích tại sao một số giày được thiết kế với một số lò xo rất nhỏ nằm ở dưới đế (Hình 22P.2).

Mục đích: khi người tác dụng lực lên lò xo thì lò xo sẽ xuất hiện lực đàn hồi, lực đàn hồi này có tác dụng làm giảm áp lực xuống mặt đất, thúc đẩy chuyển động của người và bảo vệ gót chân.

a)
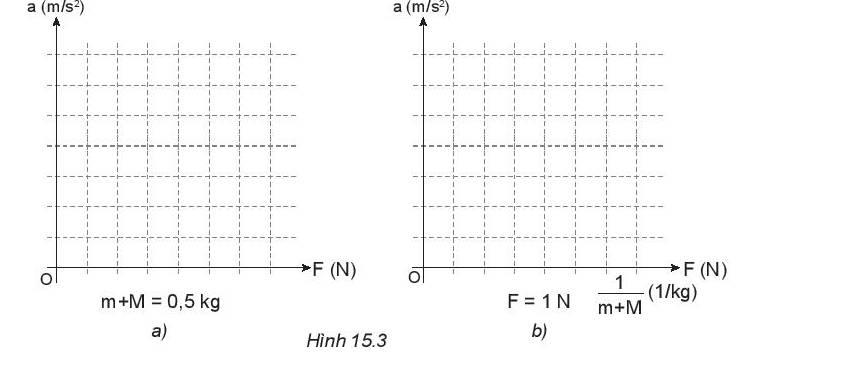
- a phụ thuộc vào F (m + M = 0, 5kg)
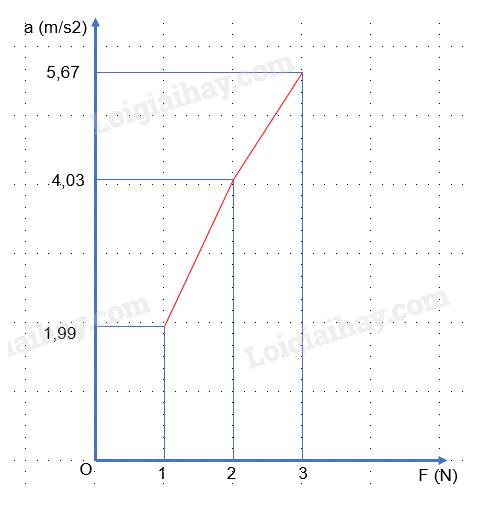
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
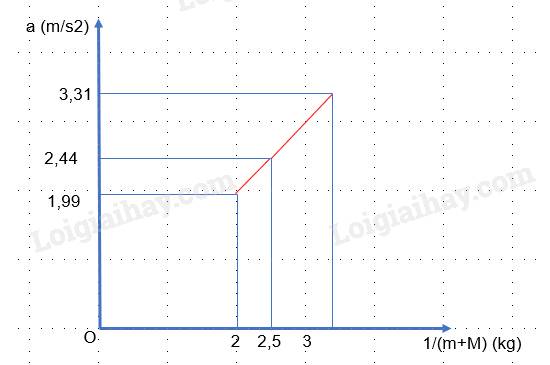
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.

Do vật chuyển động tròn đều nên tốc độ không thay đổi, hay vật dịch chuyển được các cung tròn có số đo góc bằng nhau sau những khoảng thời gian bằng nhau.

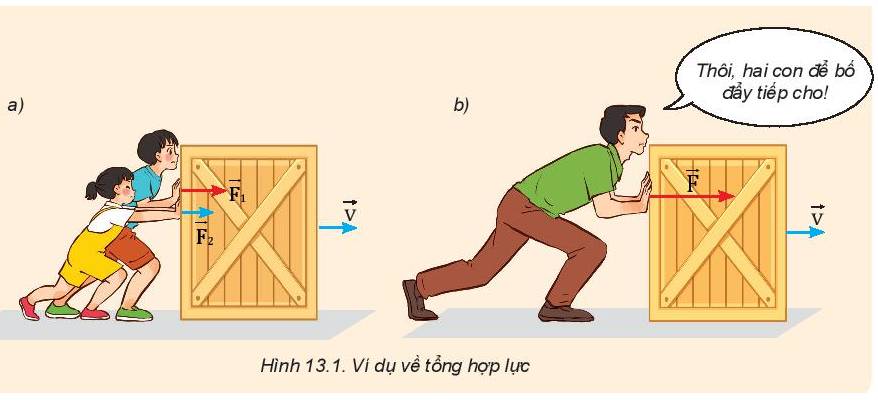
Lực đẩy của người bố trong hình có tác dụng như lực đẩy của hai anh em vì người bố khỏe, lực đẩy của bố bằng tổng lực đẩy của hai anh em cộng lại.

1.
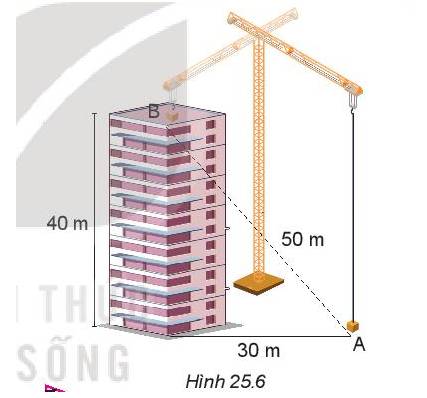
Chọn mốc thế năng tại A
Ta có m = 500 kg; g = 9,8 m/s2 ; h = 40 m.
Thế năng của khối vật liệu tại B là: Wt = m.g.h = 500.9,8.40 = 1,96.105 (J)
=> Công mà cần cẩu đã thực hiện là: A = Wt = 1,96.105 J.
2.
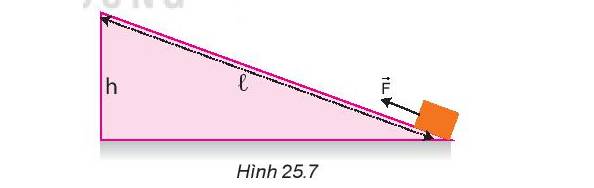
Do ma sát không đáng kể nên công của trọng lực bằng công của lực nhỏ
=> Dù lực có nhỏ hơn trọng lượng nhưng vẫn có thể đưa một vật lên cao trong mặt phẳng nghiêng.

Sử dụng công thức tính trọng lực: \(P=m
.
g\)
Ta có:
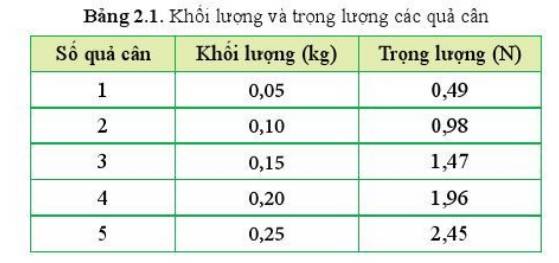
Thí nghiệm thả quả cân được thực hiện ở cùng một vị trí (vì khối lượng, trọng lượng của một quả cân là như nhau) vì vậy trong các lần đo khi thay đổi khối lượng các quả cân sẽ là như nhau.
Gia tốc rơi tự do của một quả cân khi treo là:
\(g_1=\dfrac{P_1}{m_1}=\dfrac{0,49}{0,05}=9,8\) (m/s2)
=> Gia tốc rơi tự do ở vị trí khi thức hiện phép đo là: 9,80 m/s2 (làm tròn đến 3 chữ số có nghĩa)

- Mô tả hoạt động:
Khi bắt đầu, động cơ điện từ từ kéo toa tàu lên đỉnh đầu tiên của cung đường ray. Sau đó, toa tàu trượt xuống và tăng tốc, nó chuyển động nhanh dần và có đà để di chuyển đến đỉnh thứ hai (thấp hơn đỉnh thứ nhất); sau đó tiếp tục trượt xuống và tăng tốc.
Lực kéo của động cơ thực hiện công đưa toa tàu lên đỉnh đường ray, dự trữ thế năng cực đại. Khi toa tàu này trượt xuống, động năng của nó tăng và đồng thời thế năng của nó giảm. Khi tới đáy của cung đường, toàn bộ thế năng đã chuyển hóa thành động năng, năng lượng nhiệt và năng lượng âm thanh. Khi lên dốc, động năng của toa tàu giảm, chuyển hóa thành thế năng.
Giải thích tại sao khi tàu lượn ở vị trí cao nhất của đường ray thì tốc độ của nó lại chậm nhất và ngược lại.
- Khi tàu lượn ở vị trí cao nhất của đường ray, tàu lượn có thể năng trọng trường lớn nhất, động năng nhỏ nhất nên tốc độ của nó chậm nhất. Còn khi tàu lượn ở vị trí thấp nhất của đường ray, tàu lượn có thế năng trọng trường nhỏ nhất, động năng lớn nhất nên tốc độ của nó nhanh nhất.






Lò xo nhỏ nằm dưới đế giày nhằm giảm tác dụng chịu lực của bàn chân với mặt đất, giúp đi lại nhanh hơn và dễ dàng.