K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 7 2018
đặc \(z=a+bi\) (\(a;b\in R\) và \(i^2=-1\))
ta có : \(Y=3\left|z\right|+4\left|z-4i\right|+5\left|z-3\right|\)
\(\Leftrightarrow Y=3\left|a+bi\right|+4\left|a+\left(b-4\right)i\right|+5\left|\left(a-3\right)+bi\right|\)
\(\Leftrightarrow Y=3\sqrt{a^2+b^2}+4\sqrt{a^2+\left(b-4\right)^2}+5\sqrt{\left(a-3\right)^2+b^2}\)
áp dụng bất đẳng thức Bunhiacopxki ta có :
\(Y\ge-\sqrt{\left(3^2+4^2+5^2\right)\left(a^2+b^2+a^2+\left(b-4\right)^2+\left(a-3\right)^2+b^2\right)}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3a^2+3b^2-8b-6a+25}\)
\(\Leftrightarrow Y\ge-5\sqrt{2}.\sqrt{3\left(a-1\right)^2+\left(\sqrt{3}b-\dfrac{8}{2\sqrt{3}}\right)^2+\dfrac{50}{3}}\)
dấu "=" xảy ra khi \(\dfrac{3}{\sqrt{a^2+b^2}}=\dfrac{4}{\sqrt{a^2+\left(b-4\right)^2}}=\dfrac{4}{\sqrt{\left(a-3\right)^2}+b^2}\)
giải ra tìm được \(a;b\) rồi thay ngược trở lại nha
DD
15 tháng 4 2016
giả sử z= a+ bi( a, b ϵ R)
từ giả thiết có ===> | a+ bi- 4i |+ |a+bi+4i|= 10
↔ |a+i(b-4)| +|a+(b+4)i|=10
↔ \(\sqrt{a^2+\left(b-4\right)^2}\) +\(\sqrt{a^2+\left(b+4\right)^2}\) =10
bình phương 2 vế, rút gọn thu được:
2a2+ 2b2+32+ 2\(\sqrt{\left(\left(a^2+\left(b-4\right)^2\right)\right).\left(\left(a^2+\left(b+4\right)^2\right)\right)}\)=100
bình phương tiếp:
16 tháng 6 2016
gọi z=x+yi ( x, y \(\in\) R)
ta có:\(\sqrt{\left(x^2+\left(y-4\right)^2\right)}+\sqrt{x^2+\left(y+4\right)^2}=10\)
<=> \(\sqrt{\left(x^2+\left(y-4\right)^2\right)}=10-\sqrt{x^2+\left(y+4\right)^2}\)
<=> \(x^2+\left(y-4\right)^2=100-20\sqrt{x^2+\left(y+4\right)^2}+x^2+\left(y+4\right)^2\)
<=> \(5\sqrt{\left(x^2+\left(y+4\right)^2\right)}=25+4y\)
<=> \(\begin{cases}y\ge\frac{-25}{4}\\25\left(x^2+\left(y+4\right)^2\right)=625+200y+16y^2\end{cases}\)
<=> \(\begin{cases}y\ge\frac{-25}{4}\\25x^2+25\left(y^2+8y+16\right)=625+200y+16y^2\end{cases}\)
<=>\(\begin{cases}y\ge\frac{-25}{4}\\9y^2+25x^2=225\end{cases}\)
<=>\(\begin{cases}y\ge\frac{-25}{4}\\\frac{y^2}{25}+\frac{x^2}{9}=1\end{cases}\)
ta thấy phương trình trên là một phương trình elip.
Kết luận: Vậy tập hợp điểm biểu diễn số phức Z thỏa mãn điều kiện trên là một hình elip có phương trình:
\(\frac{y^2}{25}+\frac{x^2}{9}=1\)
đúng thì tick cho mình biết nhé!!!
PT
1
CM
30 tháng 8 2019
Đặt z = a + bi. Từ z + z = 3 + 4 i suy ra
⇒ a 2 + 16 = 3 - a 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
BG
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 6 2019
Đặt \(z=x+yi\)
\(\Rightarrow\sqrt{x^2+y^2}+x+yi=3+4i\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x^2+y^2}+x=3\\y=4\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+16}+x=3\Leftrightarrow\sqrt{x^2+16}=3-x\) (\(x\le3\))
\(\Leftrightarrow x^2+16=x^2-6x+9\Rightarrow6x=-7\Rightarrow x=-\frac{7}{6}\)
\(\Rightarrow z=-\frac{7}{6}+4i\)
PT
1
CM
26 tháng 5 2017
a) Ta có z. z = z 2 nên từ z = z 3 ⇒ z 2 = z 4
Đặt z = a+ bi , suy ra:
a 4 + b 4 − 6 a 2 b 2 + 4ab( a 2 − b 2 )i = a 2 + b 2 (∗)
Do đó, ta có: 4ab( a 2 − b 2 ) = 0 (∗∗)
Từ (∗∗) suy ra các trường hợp sau:
+) a = b = 0 ⇒ z = 0
+) a = 0, b ≠ 0: Thay vào (∗), ta có b 4 = b 2 ⇒ b = 1 hoặc b = -1 ⇒ z = i hoặc z = -1
+) b = 0, a ≠ 0: Tương tự, ta có a = 1 hoặc a = -1 ⇒ z = 1 hoặc z = -1
+) a ≠ 0, b ≠ 0 ⇒ a 2 − b 2 = 0⇒ a 2 = b 2 , thay vào (∗) , ta có:
2 a 2 (2 a 2 + 1) = 0, không có a nào thỏa mãn (vì a ≠ 0 )
b) Đặt z = a + bi. Từ |z| + z = 3 + 4i suy ra
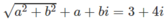
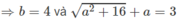
⇒ a 2 + 16 = ( 3 - a ) 2 = 9 − 6a + a 2
⇒ 6a = −7 ⇒ a = −7/6
Vậy z = −7/6 + 4i
CM
25 tháng 9 2018
Đáp án C
Phương pháp: Gọi 
là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
Lời giải chi tiết.
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng 
Khi đó ta có
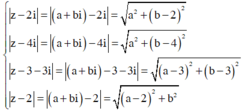
Từ giả thiết ta suy ra
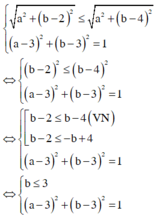
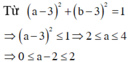
Do đó 
Đẳng thức xảy ra khi và chỉ khi
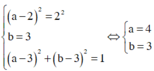
Chú ý. Đối với bài toán liên quan tới cực trị học sinh thường mắc phải sai lầm là quên tìm giá trị để cực trị xảy ra. Điều này có thể dẫn tới việc tìm sai giá trị lớn nhất nhỏ nhất
CM
17 tháng 9 2018
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng z = a+bi Khi đó ta có
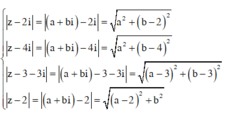
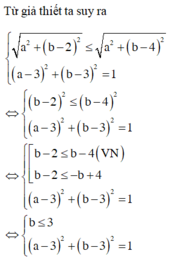
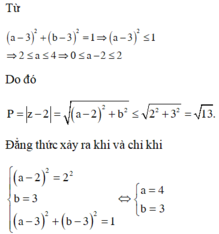
Đáp án C
goi \(z=a+bi\)
\(\Rightarrow\)\(\left|z\right|+z=3+4i\Leftrightarrow\sqrt{a^2+b^2}+a+bi=3+4i\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{a^2+b^2}+a=3\\b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}3-a\ge0\\a^2+b^2=\left(3-a\right)^2\end{matrix}\right.\\b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-7}{6}\\b=4\end{matrix}\right.\Rightarrow z=\dfrac{-7}{6}+4i\)
Cảm ơn bạn nhiều nha
