
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{x-2}{2017}+\frac{x-3}{2018}=\frac{x-4}{2019}+\frac{x-5}{2020}\)
<=> \(\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
<=> \(\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
<=> \(\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
<=> x + 2015 = 0 ( vì \(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\ne0\))
<=> x = - 2015
Vậy x = -2015.
Giải phương trình :
\(\frac{x-2}{2017}+\frac{x-3}{2018}=\frac{x-4}{2019}+\frac{x-5}{2020}\)
\(\Rightarrow\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
\(\Rightarrow\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
\(\Rightarrow\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
Mà \(\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)>0\)
\(\Rightarrow x+2015=0\)
\(\Rightarrow x=-2015\)


1) Phương trình ban đầu tương đương :
\(\left(2021x-2020\right)^3=\left(2x-2\right)^3+\left(2019x-2018\right)^3\)
Đặt \(a=2x-2,b=2019x-2018\)
\(\Rightarrow a+b=2021x-2020\)
Khi đó phương trình có dạng :
\(\left(a+b\right)^3=a^3+b^3\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow3\cdot\left(2x-2\right)\cdot\left(2019x-2018\right)\cdot\left(2021x-2002\right)=0\)
\(\Leftrightarrow\)Hoặc \(2x-2=0\)
Hoặc \(2019x-2018=0\)
Hoặc \(2021x-2020=0\)
\(\Rightarrow x\in\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\) (thỏa mãn)
Vậy : phương trình đã cho có tập nghiệm \(S=\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\)
\(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\)
\(\Leftrightarrow2x^2-3x+x^2-xm=3x^2+x-m\)
\(\Leftrightarrow-3x-xm=x-m\)
\(\Leftrightarrow4x+xm=m\Leftrightarrow x\left(4+m\right)=m\)
\(\Leftrightarrow x=\frac{m}{m+4}\)
Phương trình có nghiệm không âm \(\Leftrightarrow x\ge0\)
\(\Rightarrow\frac{m}{m+4}\ge0\)
Mà \(m+4>m\)nên \(\orbr{\begin{cases}m\ge0\\m+4\le0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-4\end{cases}}\)

\(\Leftrightarrow\left(\dfrac{x+1}{2022}+1\right)+\left(\dfrac{x+3}{2020}+1\right)+\left(\dfrac{x+5}{2018}+1\right)+\left(\dfrac{x+7}{2016}+1\right)=0\)
=>x+2023=0
=>x=-2023

Ta có:\(\frac{x-2}{2017}+1+\frac{x-3}{2018}+1=\frac{x-4}{2019}+1+\frac{x-5}{2020}+1\)
\(\Rightarrow\frac{x+2015}{2017}+\frac{x+2015}{2018}-\frac{x+2015}{2019}-\frac{x+2015}{2020}=0\)
\(\Rightarrow\left(x+2015\right)\left(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}\right)=0\)
Mà \(\frac{1}{2017}+\frac{1}{2018}-\frac{1}{2019}-\frac{1}{2020}>0\)
\(\Rightarrow x+2015=0\Rightarrow x=-2015\)
\(S=\left\{-2015\right\}\)

Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)
Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)
PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)
Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm


\(\Rightarrow x+1+2x-2020=3x-2019\Leftrightarrow3x-2019=3x-2019\)
Vậy pt có vô số nghiệm

\(x^3+2x=2018-y^2\Leftrightarrow x^3-x+3x=2018-y^2\Leftrightarrow x\left(x-1\right)\left(x+1\right)=2018-y^2-3x\)
\(VT⋮3\Rightarrow2018-y^2-3x⋮3\Leftrightarrow2018-y^2⋮3mà:2018\text{ chia 3 d}ư\text{ 2}\Rightarrow y\text{ chia 3 d}ư\text{ 2(voli)}.\text{Vậy: ko tìm đc x,y}\)
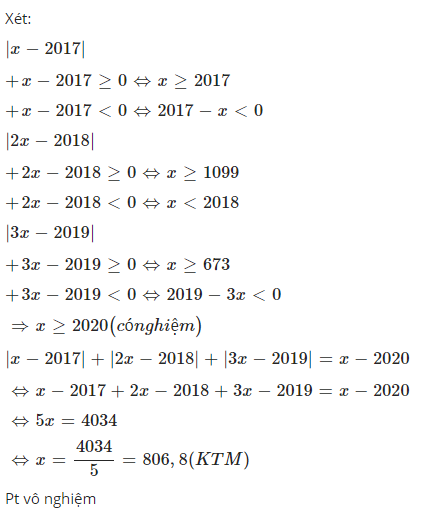

\(\left(x-2018\right)^3+\left(x-2020\right)^3=\left(2x-4038\right)\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=0^{^{\left(1\right)}}\)
Áp dụng bđt \(a+b+c=0\Leftrightarrow a^3+b^3+c^3=3abc\)
Ta có \(\left(x-2018\right)+\left(x-2020\right)+\left(4038-2x\right)=0\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=3\left(x-2018\right)\left(x-2020\right)\left(4038-2x\right)\)
Do đó (1) \(\Leftrightarrow3\left(x-2018\right)\left(x-2020\right)\left(4038-x\right)=0\)
<=> x-2018 =0 hoặc x-2020 = 0 hoặc 4038 -2x =0
<=> x=2018 hoặc x=2020 hoặc x=2019
Vậy phương trình đã cho có nghiệm S={2018;2020;2019}
\(\left(x-2018\right)^3+\left(x-2020\right)^3=\left(2x-4038\right)^3\)
\(\Leftrightarrow\left(x-2018\right)^3+\left(x-2020\right)^3+\left(4038-2x\right)^3=0\)
ta có \(\left(x-2018\right)+\left(x-2020\right)+\left(4038-2x\right)=0\)
nên đặt \(\left(x-2018\right)=a;\left(x-2020\right)=b;\left(4038-2x\right)=c\Leftrightarrow a+b+c=0\)
Khi đó a3 + b3+c3 = 0 ( 1)
mà a+b+c=0 \(\Leftrightarrow\)a+b=-c
\(\Leftrightarrow\)(a+b)3 = -c3
\(\Leftrightarrow\)a3+b3+c3 = 3abc (2)
Từ (1) và (2) \(\Leftrightarrow\)abc=0
\(\Leftrightarrow\)\(\left(x-2018\right)=0hoặc\left(x-2020\right)=0hoặc\left(4038-2x\right)=0\)
\(\Leftrightarrow\)\(x=2018hoặcx=2020hoặcx=2019\)
Vậy tập nghiệm của PT là S={2018;2019;2020}