TL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
9 tháng 5 2015
a, Với m=2 thì phương trình (1) trở thành
x mũ 2 + 2(2+2)x +4.2 -1 =0
<=> x mũ 2 + 8x +7 =0
<=> x mũ 2 + x + 7x +7 =0
<=> (x+1)(x+7) =0
<=> x= -1 hoặc x= -7
b, Ta có:
penta' = (m+2)mũ2 - 4m -1
= m m 2 +4m +4 -4m -1
= m mũ2 +3
vì m mũ2 luôn > hoặc = 0 với mọi m
suy ra m mũ2 +3 luôn >0 với mọi m
suy ra penta' >0 hay có hai nghiệm phân biệt (đpcm)
CÒN PHẦN SAU THÌ MK KO BIẾT LÀM .... THÔNG CẢM
QR
4 tháng 11 2016
a, Ta có: \(\sqrt[3]{2x+1}+\sqrt[3]{x}=1\)
↔ \(\left(\sqrt[3]{2x+1}+\sqrt[3]{x}\right)^3=1^3\)
↔\(2x+1+x+3\sqrt[3]{\left(2x+1\right)x}\left(\sqrt[3]{2x+1}+\sqrt[3]{x}\right)=1\)
↔\(3x+1+3\sqrt[3]{\left(2x+1\right)x}=1\)
↔ \(x+\sqrt[3]{\left(2x+1\right)x}=0\)
↔\(\sqrt[3]{\left(2x+1\right)x}=-x\)
↔ \(\left(2x+1\right)x=-x^3\)
↔\(x^3+2x^2+x=0\)
↔ \(x\left(x+1\right)^2=0\)
↔ \(x=0\) hoặc \(x+1=0\)
↔ \(x=0\) hoặc \(x=-1\)
b,ĐKXĐ: \(x\) khác 0, \(x\) >\(\frac{2}{3}\)
Áp dụng bất đẳng thức Cô-si cho 2 số dương \(\frac{x}{\sqrt{3x-2}}\) và \(\frac{\sqrt{3x-2}}{x}\) ta được:
\(\frac{x}{\sqrt{3x-2}}+\frac{\sqrt{3x-2}}{x}\ge2\sqrt{\frac{x}{\sqrt{3x-2}}.\frac{\sqrt{3x-2}}{x}}\)
↔\(\frac{x}{\sqrt{3x-2}}+\frac{\sqrt{3x-2}}{x}\ge2\)
Dấu "=" xảy ra\(\Leftrightarrow\) \(x=1\) hoặc \(x=2\)
Vậy tập nghiệm của pt là S={1;2}
SK
1
28 tháng 3 2019
\(\frac{3x+1}{2}-x=1\)
\(\Leftrightarrow\frac{3x+1}{2}-\frac{2x}{2}=\frac{2}{2}\)
\(\Rightarrow3x+1-2x=2\)
\(\Leftrightarrow3x-2x=2-1\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm của pt là S={1}
T
1
8 tháng 12 2015
=>(x-4) y =x2 -3x +1
+ nếu x =4 => x2 -3x +1 không có nghiệm nghuyên.
+ Nếu x khác 4 => \(y=\frac{x^2-3x+1}{x-4}=x+1+\frac{5}{x-4}\)
x ;y thuộc z => x-4 thuộc U(5) ={-5;-1;1;5}
| x-4 | -5 | -1 | 1 | 5 |
| x | -1 | 3 | 5 | 9 |
| y | -1 | -1 | 11 | 11 |
PT
1
CM
10 tháng 12 2017
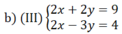
Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: 5y = 5
Do đó
QUẢNG CÁO
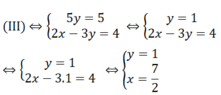
Vậy hệ phương trình có nghiệm duy nhất (7/2;1)
25 tháng 9 2020
Câu 1:
Đặt phương trình là (1)
ĐK: \(3x-16y-24\ge0\)
\(3x-16y-24=\sqrt{9x^2+16x+32}\Leftrightarrow\left(3x-16y-24\right)^2=9x^2+16x+32\)
\(\Leftrightarrow9\left(3x-16y-24\right)^2=9\left(9x^2+16x+32\right)\)\(\Leftrightarrow\left(9x-48y-72\right)^2=81x^2+144x+288\)
Với x, y nguyên thì (3y+5) là ước của (-7) và chia cho 3 dư 2
=> (3y+5)=-1 hoặc (3y+5)=-7
+ TH1: \(\left(3y+5\right)=-1\Leftrightarrow y=-2\Rightarrow x=-1\)
+ TH2: \(\left(3y+5\right)=-7\Leftrightarrow y=-4\Rightarrow x=-7\)
Vậy các cặp nghiệm nguyên của (x;y) là: (-1;-2); (-7;-4)
\(\Leftrightarrow\left(9x-48y-72\right)^2=\left(9x+8\right)^2+224\)
\(\Leftrightarrow\left(9x-48y-72\right)^2-\left(9x+8\right)^2=224\)
\(\Leftrightarrow\left(9x-48y-72+9x-8\right)\left(9x-48y-72-9x-8\right)=224\)
\(\Leftrightarrow\left(18x-48y-64\right)\left(-48y-80\right)=224\)
\(\Leftrightarrow-32\left(9x-24y-32\right)\left(3y+5\right)=224\)
\(\Leftrightarrow\left(9x-24y-32\right)\left(3y+5\right)=-7\)
25 tháng 9 2020
giả sử a là nghiệm chung của 2 phương trình
\(x^2+\text{ax}+bc=0\left(1\right)\) và \(x^2+bx+ca=0\left(2\right)\)
Ta có: \(\hept{\begin{cases}a^2+a\alpha+bc=0\\a^2+b\alpha+ca=0\end{cases}}\)
\(\Rightarrow\alpha\left(a-b\right)+c\left(b-a\right)=0\Rightarrow\left(a-c\right)\left(a-b\right)=0\Rightarrow\alpha=c\ne0\)
Thay \(\alpha=c\)vào (1) ta có: \(c^2+ac+bc=0\Rightarrow c\left(a+b+c\right)=0\Rightarrow a+b+c=0\)
Mặt khác, theo định lý Viet phương trình(1) còn có nghiệm nữa là b, phương trình(2) còn có nghiệm nữa là a. Theo định lý Viet đảo, a và b là hai nghiệm của phương trình \(x^2-\left(a+b\right)x+ab=0\Leftrightarrow x^2+cx+ab=0\left(\text{đ}pcm\right)\)
\(x^2-3x+1=0\)
\(a=1,b=-3,c=1\)
\(\Delta=b^2-4ac\)\(=\left(-3\right)^2-4\times1\times1\)\(=5>0\)
\(\Rightarrow pt\)CÓ 2 NO PHÂN BIỆT
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{3-\sqrt{5}}{2}\)\(;x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{3+\sqrt{5}}{2}\)
VẬY....