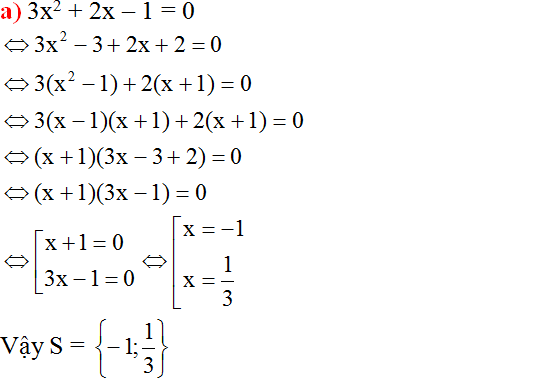Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\\ < =>3x-9+5-10x=90\)
\(< =>3x-10x=90+9-5\\ < =>-7x=94\\ < =>x=-\dfrac{94}{7}\)
b)
\(\left(2x-3\right)\left(x^2+1\right)=0\\ < =>\left[{}\begin{matrix}2x-3=0\\x^2+1=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{3}{2}\\x^2=-1\left(voli\right)\end{matrix}\right.\\ < =>x=\dfrac{3}{2}\)
c)
\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(x\ne-1;x\ne2\right)\)
suy ra: \(2\left(x-2\right)-x-1=3x-11\)
\(< =>2x-4-x-1-3x+11=0\)
\(< =>2x-x-3x=4+1-11\\ < =>-2x=-6\\ < =>x=3\left(tm\right)\)
a) \(\dfrac{x-3}{5}+\dfrac{1-2x}{3}=6\)
\(\Leftrightarrow3\left(x-3\right)+5\left(1-2x\right)=90\)
\(\Leftrightarrow-4-7x=90\)
\(\Leftrightarrow x=-\dfrac{94}{7}\)
b) \(\left(2x-3\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow2x-3=0\) (Vì \(x^2+1>0\))
\(\Leftrightarrow x=\dfrac{3}{2}\)
c) \(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\left(Đk:x\ne-1;x\ne2\right)\)
\(\Leftrightarrow2\left(x-2\right)-\left(x+1\right)=3x-11\)
\(\Leftrightarrow x-5=3x-11\)
\(\Leftrightarrow x=3\)

Câu 1a : tự kết luận nhé
\(2\left(x+3\right)=5x-4\Leftrightarrow2x+6=5x-4\Leftrightarrow-3x=-10\Leftrightarrow x=\frac{10}{3}\)
Câu 1b : \(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)ĐK : \(x\ne\pm3\)
\(\Leftrightarrow x+3-2x+6=5-2x\Leftrightarrow-x+9=5-2x\Leftrightarrow x=-4\)
c, \(\frac{x+1}{2}\ge\frac{2x-2}{3}\Leftrightarrow\frac{x+1}{2}-\frac{2x-2}{3}\ge0\)
\(\Leftrightarrow\frac{3x+3-4x+8}{6}\ge0\Rightarrow-x+11\ge0\Leftrightarrow x\le11\)vì 6 >= 0
1) 2(x + 3) = 5x - 4
<=> 2x + 6 = 5x - 4
<=> 3x = 10
<=> x = 10/3
Vậy x = 10/3 là nghiệm phương trình
b) ĐKXĐ : \(x\ne\pm3\)
\(\frac{1}{x-3}-\frac{2}{x+3}=\frac{5-2x}{x^2-9}\)
=> \(\frac{x+3-2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\frac{5-2x}{\left(x-3\right)\left(x+3\right)}\)
=> x + 3 - 2(x - 3) = 5 - 2x
<=> -x + 9 = 5 - 2x
<=> x = -4 (tm)
Vậy x = -4 là nghiệm phương trình
c) \(\frac{x+1}{2}\ge\frac{2x-2}{3}\)
<=> \(6.\frac{x+1}{2}\ge6.\frac{2x-2}{3}\)
<=> 3(x + 1) \(\ge\)2(2x - 2)
<=> 3x + 3 \(\ge\)4x - 4
<=> 7 \(\ge\)x
<=> x \(\le7\)
Vậy x \(\le\)7 là nghiệm của bất phương trình
Biểu diễn
-----------------------|-----------]|-/-/-/-/-/-/>
0 7

a) \(\dfrac{x}{3}-\dfrac{2x+1}{2}=\dfrac{x}{6}-x\)
\(\Leftrightarrow\dfrac{2x}{6}-\dfrac{3\left(2x+1\right)}{6}=\dfrac{x}{6}=\dfrac{6x}{6}\)
\(\Leftrightarrow2x-3\left(2x+1\right)=x-6x\)
\(\Leftrightarrow2x-6x-3=x-6x\)
\(\Leftrightarrow2x-6x-x+6x=3\)
\(\Leftrightarrow x=3\)
\(S=\left\{3\right\}\)
b) \(\dfrac{2+x}{5}-0,5x=\dfrac{1-2x}{4}+0,25\)
\(\Leftrightarrow\dfrac{4\left(2+x\right)}{20}-\dfrac{10x}{20}=\dfrac{5\left(1-2x\right)}{20}+\dfrac{5}{20}\)
\(\Leftrightarrow4\left(2+x\right)-10x=5\left(1-2x\right)+5\)
\(\Leftrightarrow8+4x-10x=5-10x+5\)
\(\Leftrightarrow4x-10x+10x=5+5-8\)
\(\Leftrightarrow4x=2\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
\(S=\left\{\dfrac{1}{2}\right\}\)

a) 1x−3+3=x−32−x1x−3+3=x−32−x ĐKXĐ: x≠2x≠2
Khử mẫu ta được: 1+3(x−2)=−(x−3)⇔1+3x−6=−x+31+3(x−2)=−(x−3)⇔1+3x−6=−x+3
⇔3x+x=3+6−13x+x=3+6−1
⇔4x = 8
⇔x = 2.
x = 2 không thỏa ĐKXĐ.
Vậy phương trình vô nghiệm.
b) 2x−2x2x+3=4xx+3+272x−2x2x+3=4xx+3+27 ĐKXĐ:x≠−3x≠−3
Khử mẫu ta được:
14(x+3)−14x214(x+3)−14x2= 28x+2(x+3)28x+2(x+3)
⇔14x2+42x−14x2=28x+2x+6⇔14x2+42x−14x2=28x+2x+6
⇔

a) ĐKXĐ: x # 1
Khử mẫu ta được: 2x - 1 + x - 1 = 1 ⇔ 3x = 3 ⇔ x = 1 không thoả mãn ĐKXĐ
Vậy phương trình vô nghiệm.
b) ĐKXĐ: x # -1
Khử mẫu ta được: 5x + 2x + 2 = -12
⇔ 7x = -14
⇔ x = -2
Vậy phương trình có nghiệm x = -2.
c) ĐKXĐ: x # 0.
Khử mẫu ta được: x3 + x = x4 + 1
⇔ x4 - x3 -x + 1 = 0
⇔ x3(x – 1) –(x – 1) = 0
⇔ (x3 -1)(x - 1) = 0
⇔ x3 -1 = 0 hoặc x - 1 = 0
1) x - 1 = 0 ⇔ x = 1
2) x3 -1 = 0 ⇔ (x - 1)(x2 + x + 1) = 0
⇔ x = 1 hoặc x2 + x + 1 = 0 ⇔ \(\left(x+\dfrac{1}{2}\right)^2=-\dfrac{3}{4}\) (vô lí)
Vậy phương trình có nghiệm duy nhất x = 1.
d) ĐKXĐ: x # 0 -1.
Khử mẫu ta được x(x + 3) + (x + 1)(x - 2) = 2x(x + 1)
⇔ x2 + 3x + x2 – 2x + x – 2 = 2x2 + 2x
⇔ 2x2 + 2x - 2 = 2x2 + 2x
⇔ 0x = 2
Phương trình 0x = 2 vô nghiệm.
Vậy phương trình đã cho vô nghiệm

\(a,3x^2+2x-1\Leftrightarrow3x^2-x+3x-1\Leftrightarrow x\left(3x-1\right)+\left(3x-1\right)\Leftrightarrow\left(3x-1\right)\left(x-1\right)\)

ĐKXĐ : \(x\ne\left\{2;3;4;5;6\right\}\)
\(\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}+\dfrac{1}{x^2+9x+20}+\dfrac{1}{x^2+11x+30}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+5\right)}+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+5}+\dfrac{1}{x+5}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{1}{x+2}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{4}{\left(x+2\right).\left(x+6\right)}=\dfrac{1}{8}\)
\(\Leftrightarrow\left(x+2\right).\left(x+6\right)=32\)
\(\Leftrightarrow x^2+8x-20=0\)
\(\Leftrightarrow\left(x-2\right).\left(x+10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(\text{loại}\right)\\x=-10\end{matrix}\right.\Leftrightarrow x=-10\)
Vậy tập nghiệm phương trình S = {10}
a) x - 5 = 7 - x
<=> 2x = 12
<=> x = 6
Vậy tập nghiệm phương trình S = {6}
b) 3x - 15 = 2x(x - 5)
<=> 3(x - 5) = 2x(x - 5)
<=> (2x - 3)(x - 5) = 0
<=> \(\left[{}\begin{matrix}2x-3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=5\end{matrix}\right.\)
Tập nghiệm phương trình \(S=\left\{\dfrac{3}{2};5\right\}\)