NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HA
1
YN
27 tháng 11 2021
Answer:
\(\left(x^2+x+2\right).\left(x^2+x+3\right)=6\)
Ta có: \(x^2+x+2=\left(x+\frac{1}{2}\right)^2+\frac{7}{4}>0\forall x\)
Ta đặt: \(a=x^2+x+2\left(a>0\right)\)
Lúc này phương trình trở thành:
\(a.\left(a+1\right)=6\)
\(\Rightarrow a^2+a=6\)
\(\Rightarrow a^2+a-6=0\)
\(\Rightarrow a^2+3a-2a-6=0\)
\(\Rightarrow a.\left(a+3\right)-2.\left(a+3\right)=0\)
\(\Rightarrow\left(a-2\right).\left(a+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}a-2=0\\a+3=0\end{cases}}\Rightarrow\orbr{\begin{cases}a=2\\a=-3\text{(Loại)}\end{cases}}\)
Với \(a=2\)
\(\Rightarrow x^2+x+2=2\)
\(\Rightarrow x^2+x+2-2=0\)
\(\Rightarrow x^2+x=0\)
\(\Rightarrow x.\left(x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
PT
2
14 tháng 2 2020
ghi rõ lại đề bạn mk không hiểu là 1/2 * (x+1) hay 1/2(x+1)
4 tháng 2 2020
\(\left(x^2-x+1\right)+\left(x^2-2x+3\right)+...+\left(x^2-100x+199\right)=300\)
\(\Leftrightarrow100x^2-100x+\frac{\left[\left(199-1\right):2+1\right]\left(199+1\right)}{2}=300\)
\(\Leftrightarrow100x^2-100x+10000=300\)
\(\Leftrightarrow100x^2-100x+9700=0\)
\(\Leftrightarrow100\left(x^2-x+97\right)=0\)
\(\Leftrightarrow x^2-x+97=0\)
\(\Leftrightarrow x^2-2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}+97=0\)
\(\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{387}{4}=0\left(1\right)\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0;\forall x\)
\(\Rightarrow\left(x-\frac{1}{2}\right)^2+\frac{387}{4}\ge\frac{387}{4}>0;\forall x\)
\(\Rightarrow\)pt\(\left(1\right)\)vô nghiệm
Vậy pt trên vô nghiệm
7 tháng 7 2016
pt: \(\left(1-2x\right)\left(x+3\right)\left(x^2+2\right)=0\)\(\Leftrightarrow\hept{\begin{cases}1-2x=0\\x+3=0\\x^2+2=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\x=-3\\x^2=-2\left(loại\right)\end{cases}}\)
vậy: \(x=\frac{1}{2}\),\(x=-3\)
NT
1
12 tháng 7 2017
Lời giải của bạn Hòa như trên là sai. Vì bạn đã chia cả hai vế của phương trinh cho x mà chưa biết là x = 0 hay \(x\ne0\)
Nếu \(x\ne0\)thì lời giải như trên là chính xác.
Nếu x = 0 thì phương trình có một nghiệm là 0.
18 tháng 7 2017
Nguyễn Việt Hoàng
Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
⇔ x(x + 2) - x(x + 3) = 0 (chuyển vế)
⇔ x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
⇔ x.(-1) = 0
⇔ x = 0)
NH
1
18 tháng 12 2019
\(\text{a) Thay a = 4 vào pt ta có:}\)
\(\frac{x+4}{x+2}+\frac{x-2}{x-4}=2\)
\(\Leftrightarrow\frac{\left(x-4\right)\left(x+4\right)+\left(x-2\right)\left(x+2\right)}{\left(x+2\right)\left(x-4\right)}=2\)
\(\Leftrightarrow\frac{x^2-16+x^2-4}{x^2-4x+2x-8}=2\)
\(\Leftrightarrow\frac{2x^2-20}{x^2-2x-8}=2\)
\(\Leftrightarrow2x^2-20=2.\left(x^2-2x-8\right)\)
\(\Leftrightarrow2x^2-20=2x^2-4x-16\)
\(\Leftrightarrow2x^2-2x^2+4x=-16+20\)
\(\Leftrightarrow4x=4\)
\(\Leftrightarrow x=1\)
\(\text{b) Thay x = -1 vào pt ta có:}\)
\(\frac{-1+a}{-1+2}+\frac{-1-2}{-1-a}=2\)
\(\Leftrightarrow\frac{a-1}{1}+\frac{-3}{-\left(a+1\right)}=2\)
\(\Leftrightarrow\left(a-1\right)+\frac{3}{a+1}=2\)
\(\Leftrightarrow\frac{\left(a-1\right)\left(a+1\right)+3}{a+1}=2\)
\(\Leftrightarrow\frac{a^2-1+3}{a+1}=2\)
\(\Leftrightarrow a^2+2=2.\left(a+1\right)\)
\(\Leftrightarrow a^2+2=2a+2\)
\(\Leftrightarrow a^2-2a=2-2\)
\(\Leftrightarrow a\left(a-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a=0\\a-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=0\\a=2\end{cases}}}\)
Vậy để pt có nghiệm là x = 1 thì a = {0 ; 2}
18 tháng 12 2019
\(a.Thay:a=4\Leftrightarrow\frac{x+4}{x+2}+\frac{x-2}{x-4}=2\)
\(\Leftrightarrow\frac{\left(x+4\right)\left(x-4\right)}{\left(x+2\right)\left(x-4\right)}+\frac{\left(x-2\right)\left(x+2\right)}{\left(x-4\right)\left(x+2\right)}=\frac{2\left(x+2\right)\left(x-4\right)}{\left(x+2\right)\left(x-4\right)}\)
\(\Rightarrow\left(x+4\right)\left(x-4\right)+\left(x-2\right)\left(x+2\right)=2\left(x+2\right)\left(x-4\right)\)
\(\Leftrightarrow x^2-4x+4x-16+x^2+2x-2x-4=\left(2x+4\right)\left(x-4\right)\)
\(\Leftrightarrow2x^2-20=2x^2-8x+4x-16\)
\(\Leftrightarrow2x^2-20-2x^2+8x-4x+16=0\)
\(\Leftrightarrow4x-4=0\)
\(\Leftrightarrow x=1\)
28 tháng 1 2016
Ta cm BĐT :
\(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
<=> \(3a^2+3b^2+3c^2-a^2-b^2-c^2-2ab-2bc-2ac\ge0\)
<=> \(2a^2-2ab+2b^2-2bc+2c^2-2ac\ge0\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2\ge0\)
<=> \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) (luôn đúng với mọi a ; b; c )
Dấu '' = '' BĐT xảy ra khi a =b =c
(*) ÁP dụng BĐT với \(a=x^2;b=x;c=1\) ta có
( VẾ trái ) = \(\left(x^2+x+1\right)^2\le3\left[\left(x^2\right)^2+x^2+1\right]=3\left(x^4+X^2+1\right)=\left(vế\right)phải\)
Dấu ' = '' xảy ra khi \(x^2=x=1\Leftrightarrow x=1\)
Vậy pt có n* duy nhất là 1
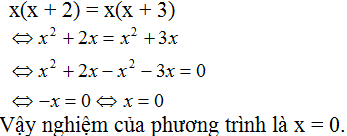
\(\dfrac{x-3}{x-2}+\dfrac{x+2}{x}=2\)
Điều kiện: \(x\ne2;x\ne0\)
\(\Leftrightarrow\dfrac{x\left(x-3\right)}{x\left(x-2\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}=\dfrac{2x\left(x-2\right)}{x\left(x-2\right)}\)
\(\Rightarrow x\left(x-3\right)+\left(x-2\right)\left(x+2\right)=2x\left(x-2\right)\)
\(\Leftrightarrow x^2-3x+x^2-4=2x^2-4x\)
\(\Leftrightarrow2x^2+3x-4=2x^2-4x\)
\(\Leftrightarrow x=4\)