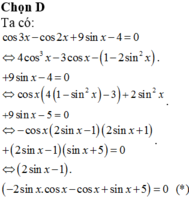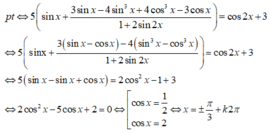Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) <=> 4sinxcosx -(2cos2x-1)=7sinx+2cosx-4
<=> 2cos2x+(2-4sinx)cosx+7sinx-5=0
- sinx=1 => 2cos2x-2cosx+2=0
pt trên vn
b) <=> 2sinxcosx-1+2sin2x+3sinx-cosx-1=0
<=> cos(2sinx-1)+2sin2x+3sinx-2=0
<=> cosx(2sinx-1)+(2sinx-1)(sinx+2)=0
<=> (2sinx-1)(cosx+sinx+2)=0
<=> sinx=1/2 hoặc cosx+sinx=-2(vn)
<=> x= \(\frac{\pi}{6}+k2\pi\) hoặc \(x=\frac{5\pi}{6}+k2\pi\left(k\in Z\right)\)

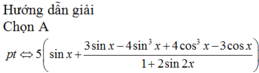
=cos2x+3

=cos2x+3 (*)
Ta có: 3( sin x – cosx) – 4 ( sin3x - cos3x)
= 3(sinx – cosx) – 4(sinx – cosx ).(sin2x + sinx. cosx+ cos2 x)
= 3( sin x – cosx) – 4(sinx – cosx).(1+ sinx. cosx)
= (sin x – cosx) . ( 3- 4 – 4sinx. cosx)
= ( sinx – cosx). (- 1- 4sinx. cosx) = - ( sinx – cosx)( 1+ 2sin2x)
Khi đó (*) trở thành
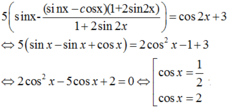
![]()

Pt \(\Leftrightarrow\left(2sinx-1\right)\left(2sin2x-1\right)=3-4\left(1-sin^2x\right)\)
\(\Leftrightarrow2sin2x\left(2sinx-1\right)-2sinx+1=-1+4sin^2x\)
\(\Leftrightarrow2sin2x\left(2sinx-1\right)-\left(4sin^2x+2sinx-2\right)=0\)
\(\Leftrightarrow2sin2x\left(2sinx-1\right)-2\left(2sinx-1\right)\left(sinx+1\right)=0\)
\(\Leftrightarrow2\left(2sinx-1\right)\left(sin2x-sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\left(1\right)\\sin2x=sinx+1\left(2\right)\end{matrix}\right.\)
Từ (1) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\),\(k\in Z\)
Từ (2)\(\Leftrightarrow2sinx.cosx-sinx-1=0\)
(Cái này tạm thời nghĩ ko ra,tối làm :)
\(sin2x=sinx+1\)
\(\Rightarrow\left\{{}\begin{matrix}sin2x\ge0\\sin^22x=\left(sinx+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ge0\\4sin^2x.cos^2x=\left(sinx+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ge0\\4sin^2x\left(1-sin^2x\right)=\left(sinx+1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ge0\\\left(sinx+1\right)\left(4sin^2x-4sin^3x-sinx-1\right)=0\end{matrix}\right.\)
Bấm máy thấy pt \(-4sin^3x+4sin^2x-sinx-1=0\) có một nghiệm \(sinx< 0\) không thỏa mãn \(sin2x\ge0\)
(Hoặc thử sd phương pháp cardano xem, chắc sẽ tìm được cụ thể nghiệm)
\(\Rightarrow sinx=-1\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\) (\(k\in Z\))
Vậy...

c/
\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}-\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow sinx=\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k2\pi\\x=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
d/
\(\Leftrightarrow sin2x-2cos2x-5=2sin2x-cos2x-6\)
\(\Leftrightarrow sin2x+cos2x=1\)
\(\Leftrightarrow\sqrt{2}sin\left(2x+\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\2x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\)
a/ ĐKXĐ:...
\(\Leftrightarrow\frac{sinx}{cosx}-\frac{\sqrt{2}}{cosx}=1\)
\(\Leftrightarrow sinx-\sqrt{2}=cosx\)
\(\Leftrightarrow sinx-cosx=\sqrt{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=\sqrt{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow x-\frac{\pi}{4}=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\frac{3\pi}{4}+k2\pi\)
b/
ĐKXĐ: ...
\(\Leftrightarrow\left(2sinx-1\right)\left(sin4x-1\right)+cos4x\left(2sinx-1\right)=0\)
\(\Leftrightarrow2sinx.sin4x-2sinx-sin4x+1+2sinx.cos4x-cos4x=0\)
\(\Leftrightarrow2sinx\left(sin4x+cos4x\right)-\left(sin4x+cos4x\right)-\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sin4x+cos4x\right)-\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sin4x+cos4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sin4x+cos4x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sin\left(4x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\4x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\4x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\frac{k\pi}{2}\\x=\frac{\pi}{8}+\frac{k\pi}{2}\left(l\right)\end{matrix}\right.\)

2 sin 2 x + sin x . cos x - cos 2 x = 3 ⇒ tan 2 x – tan x + 4 = 0
Phương trình vô nghiệm