Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có ( biểu diễn y theo x từ phương trình thứ hai):
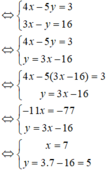
Vậy hệ phương trình có nghiệm duy nhất (7;5)

Ta có ( biểu diễn y theo x từ phương trình thứ hai):
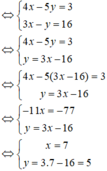
Vậy hệ phương trình có nghiệm duy nhất (7;5)

Câu a )
\(ĐKXĐx\ne-1,3\)
Ta có :
\(\frac{x}{2x+2}-\frac{2x}{x^2-2x-3}=\frac{x}{6-2x}\)
\(\Rightarrow\frac{x}{2\left(x+1\right)}-\frac{2x}{\left(x+1\right)\left(x-3\right)}=\frac{x}{-2\left(x-3\right)}\)
\(\Rightarrow\frac{x}{2\left(x+1\right)}.2\left(x+1\right)\left(x-3\right)-\frac{2x}{\left(x+1\right)\left(x-3\right)}.2\left(x+1\right)\left(x-3\right)\)
\(=-\frac{x}{2\left(x-3\right)}.2\left(x+1\right)\left(x-3\right)\)
=> x(x-3) -4x =−x(x+1)
=> \(x^2-7x=-x^2-x\)
\(\Rightarrow2x^2-6x=0\)
\(\Rightarrow2x\left(x-3\right)=0\)
\(\Rightarrow x\in\left\{3,0\right\}\)
Câu b )
Ta có :
\(\hept{\begin{cases}\sqrt{2}x-3y=2006\\2x+\sqrt{3}y=2007\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt{2}x-3y=2006\\2\sqrt{3}x+3y=2007\sqrt{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt{2}x-3y=2006\\2\sqrt{3}x+3y+\sqrt{2}x-3y=2007\sqrt{3}+2006\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\sqrt{2}x-3y=2006\\\left(\sqrt{2}+2\sqrt{3}\right)x=2007\sqrt{3}+2006\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=\frac{\sqrt{2}x-2006}{3}\\x=\frac{2007\sqrt{3}+2006}{\sqrt{2}+2\sqrt{3}}\end{cases}}\)
\(\hept{\begin{cases}y=\frac{\sqrt{2}.\frac{2007\sqrt{3}+2006}{\sqrt{2}+2\sqrt{3}}-2006}{3}\\x=\frac{2007\sqrt{3}+2006}{\sqrt{2}+2\sqrt{3}}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}y=\frac{2007\sqrt{6}-4012\sqrt{3}}{\left(\sqrt{2}+2\sqrt{3}\right).3}\\x=\frac{2007\sqrt{3}+2006}{\sqrt{2}+2\sqrt{3}}\end{cases}}\)

\(\left\{{}\begin{matrix}2x+y=3\\3x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3-2x\\3x-\left(3-2x\right)=2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}y=3-2x\\x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=1\end{matrix}\right.\)
Vậy hpt trên có nghiệm duy nhất là (1;1)
\(\left\{{}\begin{matrix}4x+y=3\\x-y=2\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}4x+y=3\\x=2+y\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}4\left(2+y\right)+y=3\\x=2+y\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}8+4y+y=3\\x=2+y\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}5y=-5\\x=2+y\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}y=-1\\x=2+\left(-1\right)\end{matrix}\right.\)
\(\rightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Vậy nghiệm duy nhất của PT (1;-1)
\(\left\{{}\begin{matrix}4x+y=3\\x-y=2\end{matrix}\right.\)
từ phương tình (2)thế vào phương trình (1)
<=>\(\left\{{}\begin{matrix}4x+y=3\\x=y+2\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}4\left(y+2\right)+y=3\\x=y+2\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}4y+8+y=3\\x=y+2\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)
Vậy.........