K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 1 2022
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=5\\2x-2y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=17\\x-y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{17}{4}\\x=6+y=\dfrac{-17}{4}+6=\dfrac{7}{4}\end{matrix}\right.\)
NV
1
6 tháng 6 2017
\(\Leftrightarrow\hept{\begin{cases}\left(x^2+y^2\right)^2=-4z^2+9z-5\\\left(x-y\right)^2=4z-5\end{cases}}\)ta dễ thấy để hai phương trình có ng thì vế phải của 2 phương trình phải dương nên có hệ điều kiện :
\(\Rightarrow\hept{\begin{cases}-4z^2+9z-5\ge0\\4z-5\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(4z-5\right)\left(1-z\right)\ge0\\z\ge\frac{5}{4}\end{cases}}\)
- TH1 : \(\hept{\begin{cases}4z-5\ge0\\1-z\ge0\\z\ge\frac{5}{4}\end{cases}}\Leftrightarrow\hept{\begin{cases}z\ge\frac{5}{4}\\z\le1\\z\ge\frac{5}{4}\end{cases}}\left(vn\right)\)
- TH2: \(\hept{\begin{cases}4z-5\le0\\1-z\le0\\4z-5\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}z\le\frac{5}{4}\\z\ge1\\z\ge\frac{5}{4}\end{cases}}\Leftrightarrow z=\frac{5}{4}}\)
Ta thế \(Z=\frac{5}{4}\)vào ta có hệ \(\hept{\begin{cases}\left(x^2+y^2\right)^2=0\\\left(x-y\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2+y^2=0\\x-y=0\end{cases}\Leftrightarrow x=y=0}\)
Kết luận nghiệm \(\left(x,y,z\right)=\left(0;0;\frac{5}{4}\right)\)
10 tháng 8 2023
4:
x+3y=4m+4 và 2x+y=3m+3
=>2x+6y=8m+8 và 2x+y=3m+3
=>5y=5m+5 và x+3y=4m+4
=>y=m+1 và x=4m+4-3m-3=m+1
x+y=4
=>m+1+m+1=4
=>2m+2=4
=>2m=2
=>m=1
3:
x+2y=3m+2 và 2x+y=3m+2
=>2x+4y=6m+4 và 2x+y=3m+2
=>3y=3m+2 và x+2y=3m+2
=>y=m+2/3 và x=3m+2-2m-4/3=m+2/3
TN
0
DT
2
TN
5 tháng 9 2017
Từ \(x^2+2y=-11\Rightarrow y=-\frac{x^2}{2}-\frac{11}{2}\)
\(\left(2\right)\Leftrightarrow\left(-\frac{x^2}{2}-\frac{11}{2}\right)^4+4(2x-3)\left(-\frac{x^2}{2}-\frac{11}{2}\right)^2-32\left(-\frac{x^2}{2}-\frac{11}{2}\right)-48x-140=0\)
\(\Leftrightarrow\frac{x^8}{16}+\frac{11x^6}{4}+2x^5+\frac{339x^4}{8}+44x^3+\frac{1131x^2}{4}+194x+\frac{9409}{16}=0\)
Tới đây tìm được \(Min=\frac{1}{48}\left(4225+\sqrt[3]{1972230880321-24752089344\sqrt{4317}}+\sqrt[3]{1972230880321+24752089344\sqrt{4317}}\right)>0\)
Hay pt >0 tức vô nghiệm :v
17 tháng 9 2017
Làm sao để tìm min = 1/48 giải rùm mình từ đoạn đó đc không
KD
3
AM
20 tháng 4 2022
Có: \(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+4y=10\left(1\right)\\2x-3y=-4\left(2\right)\end{matrix}\right.\)
Lấy (1) trừ (2) vế theo vế, ta có: 7y=14 hay y=2 \(\Rightarrow x=1\)
Vậy nghiệm của hệ phương trình là (1;2)
20 tháng 4 2022
\(\left\{{}\begin{matrix}x+2y=5\\2x-3y=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+6y=15\\4x-6y=-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=7\\x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\1+2y=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
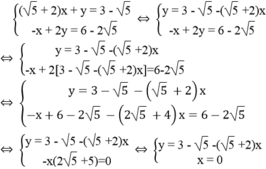
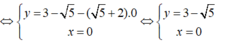
$\begin{cases}2x+y=4\\x+2y=5\end{cases}$
`<=>` $\begin{cases}2x+y=4\\2x+4y=10\end{cases}$
`<=>` $\begin{cases}3y=6\\x=5-3y\end{cases}$
`<=>` $\begin{cases}y=2\\y=1\end{cases}$
Vậy `(x,y)=(2,1)`
$\begin{cases}2x+y=4\\x+2y=5\end{cases}$
`<=>` $\begin{cases}2x+y=4\\2x+4y=10\end{cases}$
`<=>` $\begin{cases}3y=6\\x=5-2y\end{cases}$
`<=>` $\begin{cases}y=2\\y=1\end{cases}$
Vậy `(x,y)=(2,1)`