K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
C
8 tháng 5 2017
Hệ tương đương
\(\hept{\begin{cases}\left(x+y\right)^2-2xy-2\left(x+y\right)=6\\x+y-xy=5\end{cases}}\)
S = x + y, P = xy
=>
\(\hept{\begin{cases}S^2-2P-2S=6\\S-P=5\end{cases}}\)
Thay P = S - 5 vào PT trên
=> S2 - 2(S - 5) - 2S = 6
<=> S2 - 4S + 4 = 0
<=> S = 2
=> P = -3
=> x, y là 1 nghiệm của PT
X2 - 2X - 3 = 0
=>
x = -1, y = 3
Hoặc x = 3, y = -1
TN
0
NV
0
15 tháng 10 2020
Cộng theo từng vế của hai phương trình ta được:
\(x^2-y^2=\left(2y+3x-6\right)-\left(2x+3y-6\right)\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)=x-y\)
\(\Leftrightarrow\left(x+y-1\right)\left(x-y\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=y\\x=1-y\end{cases}}\)
TH1: \(x=y\)thay vào phương trình thứ nhất ta được: \(x^2=2x+3x-6\Leftrightarrow x^2-5x+6=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=3\\x=2\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}y=3\\y=2\end{cases}}\)
TH2: \(x=1-y\)thay vào phương trình thứ nhất ta được:
\(\left(1-y\right)^2=2y+3\left(1-y\right)-6\)
\(\Leftrightarrow y^2-2y+1=-y-3\)
\(\Leftrightarrow y^2-y+4=0\)(vô nghiệm)
Vậy hệ phương trình có nghiệm \(\left(x,y\right)\in\left\{\left(3;3\right),\left(2;2\right)\right\}\)
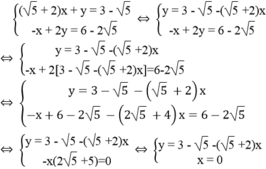
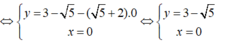
\(\Leftrightarrow\left\{{}\begin{matrix}-2x-2y=5\\2x-2y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=17\\x-y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{17}{4}\\x=6+y=\dfrac{-17}{4}+6=\dfrac{7}{4}\end{matrix}\right.\)
em cảm ơn ạ