Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Thay m=\(-\sqrt{2}\) ta được
\(\left\{{}\begin{matrix}2x-y=-\sqrt{2}\\4x-\left(-\sqrt{2}\right)^2=2\sqrt{2}\end{matrix}\right.\)\(\Leftrightarrow\)
\(\)\(\left\{{}\begin{matrix}2x-y=-\sqrt{2}\\4x+2y=2\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=-\sqrt{2}\\2x+y=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=-2\sqrt{2}\\2x+y=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
a. Với \(m=-\sqrt{2}\), ta có hệ : \(\left\{{}\begin{matrix}2x-y=-\sqrt{2}\\4x-2y=2\sqrt{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x-y=-\sqrt{2}\\2x-y=\sqrt{2}\end{matrix}\right.\)
Vậy phương trình vô nghiệm.
b. Với \(m=\sqrt{2}\), ta có hệ : \(\left\{{}\begin{matrix}2x-y=\sqrt{2}\\4x-2y=2\sqrt{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x-y=\sqrt{2}\\2x-y=\sqrt{2}\end{matrix}\right.\)
Vậy phương trình có vô số nghiệm.
c. Với \(m=1\), ta có hệ : \(\left\{{}\begin{matrix}2x-y=1\\4x-y=2\sqrt{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=2x-1\\4x-2x+1=2\sqrt{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y=2x-1\\x=\dfrac{2\sqrt{2}-1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y=2\sqrt{2}-2\\x=\dfrac{2\sqrt{2}-1}{2}\end{matrix}\right.\)
Vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(\dfrac{2\sqrt{2}-1}{2};2\sqrt{2}-2\right).\)

Hệ có nghiệm duy nhất khi và chỉ khi \(\frac{m-1}{2}\ne\frac{-m}{-1}\Leftrightarrow m\ne-1\)
Xét m=0 thì x=1, y=-3 --> thỏa mãn
Xét m khác 0 thì nhân 2 vế của đẳng thức thứ 2 cho m ---> \(\hept{\begin{cases}\left(m-1\right)x-my=3m-1\\2mx-my=m^2+5m\end{cases}}\)
Lấy đẳng thức 2 trừ đẳng thức 1 vế theo vế--> Dễ dàng tính được x=m+1, y=m-3 ---> thế vào điều kiện:
\(x^2-y^2< 4\Leftrightarrow\left(m+1\right)^2-\left(m-3\right)^2< 4\Leftrightarrow8m-8< 4\Leftrightarrow m< \frac{3}{2}\)
Đối chiếu điều kiện có nghiệm duy nhất---> Kết luận \(m< \frac{3}{2},m\ne-1\)

BẠN NÀO CÓ THỂ GIẢI CHO TỚ BÀI NÀY CHO MỘT HÌNH VUÔNG CÓ CHU VI 16 CM.LẤY MỖI CÃNH HÌNH VUÔNG LÀM ĐƯỜNG KÍNH, NGƯỜI TA VẼ 4 NỬ HÌNH TRÒN.CHÚNG GIAO NHAU TẠO THÀNH BÔNG HOA .TÍNH DIỆN TÍCH BÔNG HOA ĐÓ
Xét (I):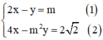
Từ phương trình (1) ta rút ra được y = 2x – m (*)
Thay (*) vào phương trình (2) ta được:
4x – m2.(2x – m) = 2√2
⇔ 4x – 2m2.x + m3 = 2√2
⇔ (4 – 2m2).x = 2√2 – m3 (**)
a) Với m = -√2, phương trình (**) trở thành: 0x = 4√2
Phương trình vô nghiệm.
Vậy với m = -√2, hệ phương trình (I) vô nghiệm.
b) Với m = √2, phương trình (**) trở thành: 0x = 0
Phương trình nghiệm đúng với mọi x ∈ R, khi đó y = 2x – √2
Vậy với m = √2, hệ (I) có vô số nghiệm dạng (x ; 2x - √2), x ∈ R
c) Với m = 1, phương trình (**) trở thành: 2x = 2√2 – 1 ⇔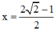
Thay vào (*) ta được:
Vậy hệ phương trình có nghiệm duy nhất