
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chắc câu c quá, tại tổng 2 ô vuông của hình chữ nhật có 10 chấm tròn. =)
Em nghĩ là câu c vì thấy tổng của các chấm tròn ở mỗi miếng đều là 10.

Đáp án b
Các hình màu xanh là phản chiếu của các hình máu cam trong gương.
Nhìn sơ sơ đoán là chọn B
Kiểu 2 hình ở gần (đáy hình cam trên và đỉnh hình xanh dưới sẽ giống nhau), 2 hình còn lại giống nhau tại vị trí đỉnh trên hình cam và đáy dưới hình xanh

b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)

1.
a. Em tự giải
b.
\(\left\{{}\begin{matrix}2x+y=4m-1\\3x-2y=-m+9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=8m-2\\3x-2y=-m+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=7m+7\\y=\dfrac{3x+m-9}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=m+1\\y=2m-3\end{matrix}\right.\)
Để \(x+y=7\Rightarrow m+1+2m-3=7\)
\(\Rightarrow3m=9\Rightarrow m=3\)
2.
a. Em tự giải
b.
Phương trình có 2 nghiệm khi:
\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\ge0\)
\(\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
Ta có:
\(P=x_1^2+x_2^2+8x_1x_2=\left(x_1+x_2\right)^2+6x_1x_2\)
\(=4\left(m+1\right)^2+6\left(2m+10\right)=4m^2+20m+64\)
\(=4\left(m^2+5m+6\right)+40=4\left(m+2\right)\left(m+3\right)+40\)
Do \(\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\) \(\Rightarrow\left(m+2\right)\left(m+3\right)\ge0\)
\(\Rightarrow P\ge40\)
Vậy \(P_{min}=40\) khi \(m=-3\)
(Nếu bài này giải là \(4m^2+20m+64=\left(2m+5\right)^2+39\ge39\) là sai vì dấu = khi đó xảy ra tại \(m=-\dfrac{5}{2}\) ko thỏa mãn điều kiện \(\Delta\) để pt có nghiệm)

Theo đề bài thì có a + b + c = 3
=> 3a + bc = (a + b + c)a + bc = a2 + ab + ac + bc = (a + b)(a + c)

\(\left(d\right):\frac{x}{a}+\frac{y}{b}=1\)\(\left(1\right)\)
Thế \(x=a,y=0\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(A\left(a,0\right)\)thuộc \(\left(d\right)\).
Thế \(x=0,y=b\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(B\left(0,b\right)\)thuộc \(\left(d\right)\).
Do đó ta có đpcm.

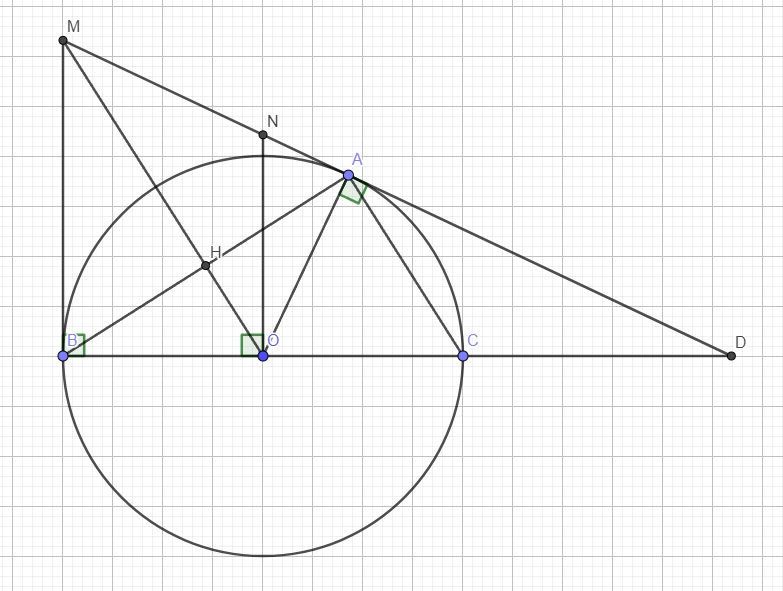
4c.
Do M là giao điểm 2 tiếp tuyến tại A và B, theo tính chất hai tiếp tuyến cắt nhau
\(\Rightarrow\widehat{OMN}=\widehat{OMB}\)
Mà \(MB||NO\) (cùng vuông góc BC) \(\Rightarrow\widehat{OMB}=\widehat{MON}\) (so le trong)
\(\Rightarrow\widehat{OMN}=\widehat{MON}\)
\(\Rightarrow\Delta OMN\) cân tại N
\(\Rightarrow MN=ON\)
Cũng theo 2 t/c 2 tiếp tuyến cắt nhau \(\Rightarrow MA=MB\)
Do MD là tiếp tuyến của (O) tại A \(\Rightarrow OA\perp MD\)
Áp dụng hệ thức lượng trong tam giác vuông OND với đường cao OA:
\(ON^2=NA.ND\Rightarrow MN^2=NA.ND\)
\(\Rightarrow MN^2=\left(MA-MN\right).ND=\left(MB-MN\right).ND\)
\(\Rightarrow MN^2=MB.ND-MN.ND\)
\(\Rightarrow MB.ND-MN^2=MN.ND\)
\(\Rightarrow\dfrac{MB.ND-MN^2}{MN.ND}=1\)
\(\Rightarrow\dfrac{MB}{MN}-\dfrac{MN}{ND}=1\) (đpcm)




.png)
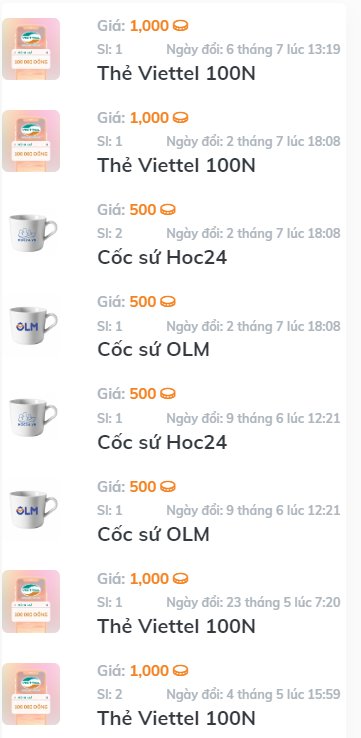

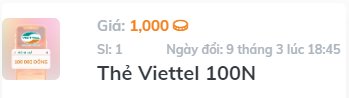
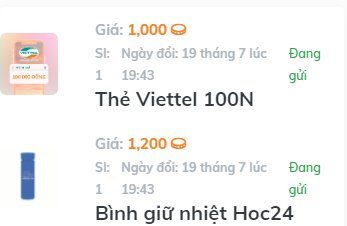
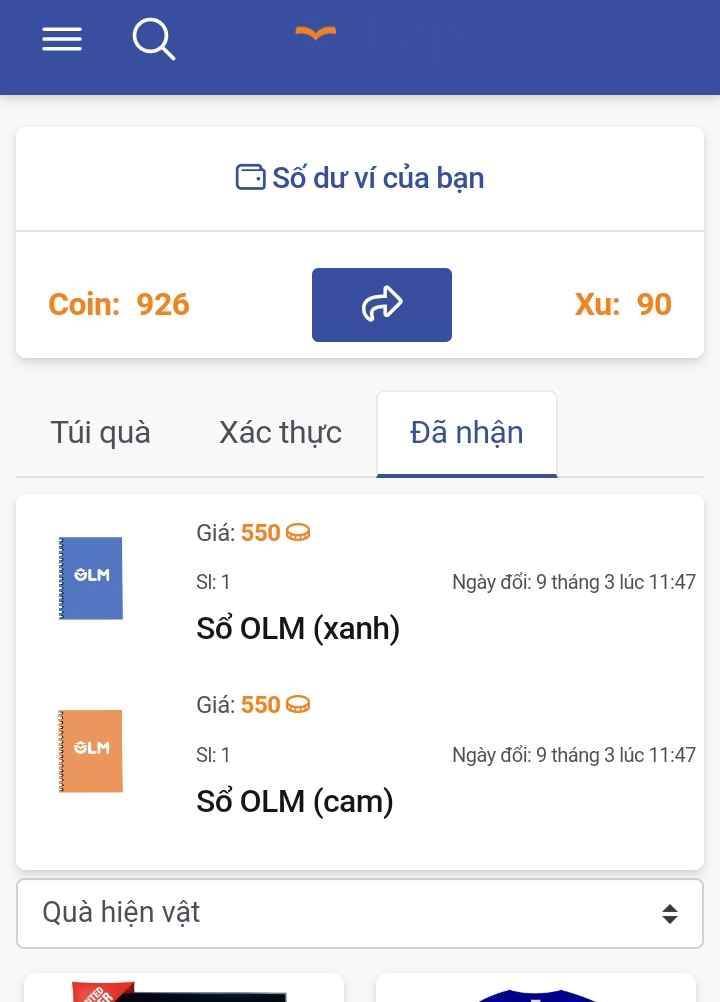
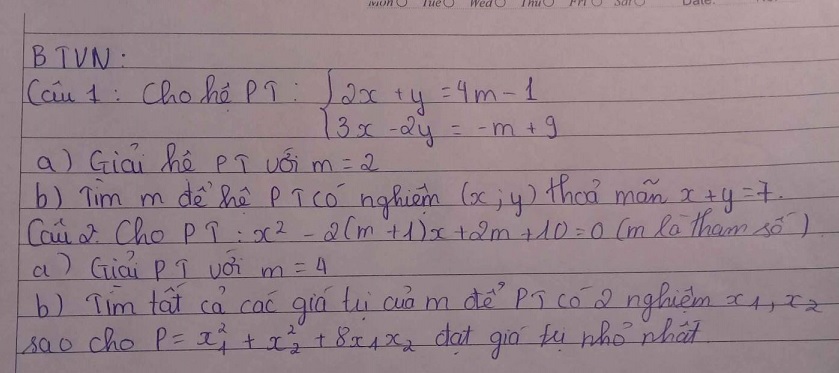


 ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
1: ĐKXĐ: x∉{0;-1}
Ta có: \(\frac{x-1}{x}+\frac{1-2x}{x\left(x+1\right)}=\frac{1}{x+1}\)
=>\(\frac{\left(x-1\right)\left(x+1\right)}{x\left(x+1\right)}+\frac{1-2x}{x\left(x+1\right)}=\frac{x}{x\left(x+1\right)}\)
=>\(\left(x-1\right)\left(x+1\right)+1-2x=x\)
=>\(x^2-1+1-2x-x=0\)
=>\(x^2-3x=0\)
=>x(x-3)=0
=>\(\left[\begin{array}{l}x=0\left(loại\right)\\ x=3\left(nhận\right)\end{array}\right.\)
2: ĐKXĐ: x∉{0;4}
ta có: \(\frac{5}{x}+\frac{x-3}{x-4}=\frac{x^2-10}{x\left(x-4\right)}\)
=>\(\frac{5\left(x-4\right)+x\left(x-3\right)}{x\left(x-4\right)}=\frac{x^2-10}{x\left(x-4\right)}\)
=>\(5\left(x-4\right)+x\left(x-3\right)=x^2-10\)
=>\(5x-20+x^2-3x=x^2-10\)
=>2x-20=-10
=>2x=10
=>x=5(nhận)
3: ĐKXĐ: x∉{0;3}
Ta có: \(\frac{x+3}{x-3}=\frac{3}{x^2-3x}+\frac{1}{x}\)
=>\(\frac{x+3}{x-3}=\frac{3}{x\left(x-3\right)}+\frac{1}{x}\)
=>\(\frac{x\left(x+3\right)}{x\left(x-3\right)}=\frac{3}{x\left(x-3\right)}+\frac{x-3}{x\left(x-3\right)}\)
=>\(x\left(x+3\right)=3+x-3=x\)
=>\(x^2+3x-x=0\)
=>\(x^2+2x=0\)
=>x(x+2)=0
=>\(\left[\begin{array}{l}x=0\\ x+2=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\left(loại\right)\\ x=-2\left(nhận\right)\end{array}\right.\)
4: ĐKXĐ: x∉{0;3}
Ta có: \(\frac{3}{x^2-3x}+\frac{1}{x}=\frac{x+4}{x-3}\)
=>\(\frac{3}{x\left(x-3\right)}+\frac{1}{x}=\frac{x+4}{x-3}\)
=>\(\frac{3+x-3}{x\left(x-3\right)}=\frac{x\left(x+4\right)}{x\left(x-3\right)}\)
=>\(x=x\left(x+4\right)\)
=>x(x+4)-x=0
=>x(x+3)=0
=>\(\left[\begin{array}{l}x=0\left(loại\right)\\ x=-3\left(nhận\right)\end{array}\right.\)
5: ĐKXĐ: x∉{0;4}
ta có: \(\frac{x+4}{x-4}-\frac{1}{x}=\frac{4}{x^2-4x}\)
=>\(\frac{x+4}{x-4}-\frac{1}{x}=\frac{4}{x\left(x-4\right)}\)
=>\(\frac{x\left(x+4\right)-\left(x-4\right)}{x\left(x-4\right)}=\frac{4}{x\left(x-4\right)}\)
=>\(x\left(x+4\right)-x+4=4\)
=>\(x^2+4x-x=0\)
=>\(x^2+3x=0\)
=>x(x+3)=0
=>\(\left[\begin{array}{l}x=0\\ x+3=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\left(loại\right)\\ x=-3\left(nhận\right)\end{array}\right.\)
6: ĐKXĐ: x∉{3;-1}
Ta có: \(\frac{x}{x-3}+\frac{x}{x+1}=\frac{2x^2-4}{\left(x-3\right)\left(x+1\right)}\)
=>\(\frac{x\left(x+1\right)+x\left(x-3\right)}{\left(x-3\right)\left(x+1\right)}=\frac{2x^2-4}{\left(x-3\right)\left(x+1\right)}\)
=>\(x\left(x+1\right)+x\left(x-3\right)=2x^2-4\)
=>\(x^2+x+x^2-3x=2x^2-4\)
=>-2x=-4
=>x=2(nhận)
7: ĐKXĐ: x∉{0;2}
ta có: \(\frac{x+2}{x-2}-\frac{6}{x}=\frac{9}{x^2-2x}\)
=>\(\frac{x+2}{x-2}-\frac{6}{x}=\frac{9}{x\left(x-2\right)}\)
=>\(\frac{x\left(x+2\right)-6\left(x-2\right)}{x\left(x-2\right)}=\frac{9}{x\left(x-2\right)}\)
=>x(x+2)-6(x-2)=9
=>\(x^2+2x-6x+12-9=0\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>\(\left[\begin{array}{l}x-1=0\\ x-3=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=1\left(nhận\right)\\ x=3\left(nhận\right)\end{array}\right.\)
8: ĐKXĐ: x∉{0;2}
ta có: \(\frac{2}{x^2-2x}+\frac{1}{x}=\frac{x+2}{x-2}\)
=>\(\frac{2}{x\left(x-2\right)}+\frac{1}{x}=\frac{x+2}{x-2}\)
=>\(\frac{2+x-2}{x\left(x-2\right)}=\frac{x\left(x+2\right)}{x\left(x-2\right)}\)
=>x(x+2)=x
=>x(x+2)-x=0
=>x(x+2-1)=0
=>x(x+1)=0
=>\(\left[\begin{array}{l}x=0\left(loại\right)\\ x=-1\left(nhận\right)\end{array}\right.\)
9: ĐKXĐ: x∉{0;-5}
\(\frac{x-5}{x}+\frac{x-3}{x+5}=\frac{x-25}{x^2+5x}\)
=>\(\frac{x-5}{x}+\frac{x-3}{x+5}=\frac{x-25}{x\left(x+5\right)}\)
=>\(\frac{\left(x-5\right)\left(x+5\right)+x\left(x-3\right)}{x\left(x+5\right)}=\frac{x-25}{x\left(x+5\right)}\)
=>\(\left(x-5\right)\left(x+5\right)+x\left(x-3\right)=x-25\)
=>\(x^2-25+x^2-3x-x+25=0\)
=>\(2x^2-4x=0\)
=>2x(x-2)=0
=>x(x-2)=0
=>\(\left[\begin{array}{l}x=0\left(loại\right)\\ x=2\left(nhận\right)\end{array}\right.\)
10:
ĐKXĐ: x∉{0;6}
\(\frac{x+6}{x-6}-\frac{6}{x^2-6x}=\frac{1}{x}\)
=>\(\frac{x+6}{x-6}-\frac{6}{x\left(x-6\right)}=\frac{1}{x}\)
=>\(\frac{x\left(x+6\right)}{x\left(x-6\right)}-\frac{6}{x\left(x-6\right)}=\frac{x-6}{x\left(x-6\right)}\)
=>\(x^2+6x-6=x-6\)
=>\(x^2+5x=0\)
=>x(x+5)=0
=>\(\left[\begin{array}{l}x=0\\ x+5=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\left(loại\right)\\ x=-5\left(nhận\right)\end{array}\right.\)
11: ĐKXĐ: x∉{0;7}
Ta có: \(\frac{x+7}{x-7}-\frac{7}{x^2-7x}=\frac{1}{x}\)
=>\(\frac{x+7}{x-7}-\frac{7}{x\left(x-7\right)}=\frac{1}{x}\)
=>\(\frac{x\left(x+7\right)-7}{x\left(x-7\right)}=\frac{x-7}{x\left(x-7\right)}\)
=>x(x+7)-7=x-7
=>x(x+7)=x
=>x(x+7)-x=0
=>x(x+6)=0
=>\(\left[\begin{array}{l}x=0\\ x+6=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=0\left(loại\right)\\ x=-6\left(nhận\right)\end{array}\right.\)
12: ĐKXĐ: x∉{0;-4}
ta có: \(\frac{x+5}{x}-\frac{x-7}{x+4}=\frac{x^2+35}{x^2+4x}\)
=>\(\frac{x+5}{x}-\frac{x-7}{x+4}=\frac{x^2+35}{x\left(x+4\right)}\)
=>\(\frac{\left(x+5\right)\left(x+4\right)-x\left(x-7\right)}{x\left(x+4\right)}=\frac{x^2+35}{x\left(x+4\right)}\)
=>\(\left(x+5\right)\left(x+4\right)-x\left(x-7\right)=x^2+35\)
=>\(x^2+9x+20-x^2+7x=x^2+35\)
=>\(x^2+35=16x+20\)
=>\(x^2-16x+15=0\)
=>(x-1)(x-15)=0
=>\(\left[\begin{array}{l}x-1=0\\ x-15=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x...