Giải giúp mình nhé!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BA
22 tháng 1 2016
A B H C
a) theo tính chất tam giác cân ta có :
Đường trung tuyến ứng với cạnh đáy đồng thời là đường cao, đường trung trực dường phân giác
=> AH là đường trung trực của BC
b) Theo CM ý a) ta có : AH là đường trung trực của BC
=> AH vuông góc với BC
=> tam giác AHB vuông tại H
=> \(AH^2+BH^2=AB^2\)
=> \(HB^2=AB^2-AH^2\)
=>
BA
22 tháng 1 2016
mình nhấn nhầm gửi để mình làm tiếp
=>\(HB^2=5^2-4^2\)
=>\(HB^2=25-16\)
=>\(HB^2=9\)
=> \(HB=3cm\)
Lại có HB = HC
mà : HB + HC = BC
=> BC = 3 + 3
=> BC = 6 cm
ta có : tam giác ABC cân tại A
=> AB = AC
Mặt khác : chu vi của tam ABC = AB + AC + BC
=> chu vi của tam ABC = 5 + 5 + 6
= 16 cm
****
VN
23 tháng 1 2017
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
VN
23 tháng 1 2017
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
19 tháng 2 2020
Đề sai à? Nếu đúng thì có phải là:
cho tam giác ABC cân tại A,hạ CM vuông góc với AB tại M, AH vuông góc BC tại H.Biết BH=2cm,AB=4cm
a)Tính AH
b)Tính chu vi tam giác ABC
c)Tính độ dài đường cao CM của tam giác ABC
d)Hạ MN vuông góc BC tại N.Tính MN
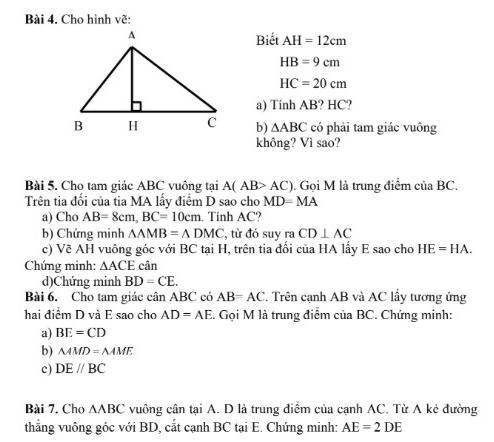
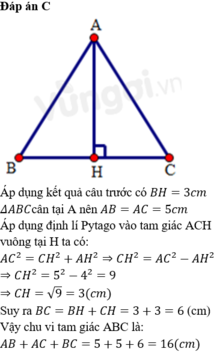
wow anh vẽ giỏi nhỉ
xuất sắc
BT1: Xét \(\Delta ABH\)vuông tại H
\(\Rightarrow AH^2+BH^2=AB^2\)( định lý Pytago )
\(\Rightarrow BH^2=AB^2-AH^2=5^2-4^2=25-16=9\)
\(\Rightarrow BH=3\left(cm\right)\)
Xét \(\Delta ABC\)cân tại A, đường cao AH \(\Rightarrow\)H là trung điểm của BC
\(\Rightarrow BC=2BH=2.3=6\)(cm)
\(\Rightarrow\)Chu vi \(\Delta ABC\)\(=AB+BC+CA=5+6+5=16\)(cm)
Vậy chu vi tam giác ABC là \(16cm\)
BT2: Xét \(\Delta DFE\)cân tại F , đường cao \(FM\)
\(\Rightarrow\)M là trung điểm DE \(\Rightarrow MD=\frac{1}{2}DE=\frac{1}{2}.8=4\)(cm)
Xét \(\Delta DMF\)vuông tại M \(\Rightarrow MD^2+MF^2=DF^2\)( định lý Pytago )
\(\Rightarrow MF^2=DF^2-MD^2=5^2-4^2=25-16=9\)
\(\Rightarrow MF=3\left(cm\right)\)
\(\Rightarrow S_{DFE}=\frac{1}{2}MF.DE=\frac{1}{2}.3.8=12\left(cm^2\right)\)
Vậy \(S_{DFE}=12cm^2\)