VT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PA
3
HL
3
8 tháng 12 2023
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)
TT
0
9 tháng 8 2018
chưa ai lm thì mèo lm nha, chọn bài dễ nhất
Bài 1:
a,\(\sqrt{4+2\sqrt{3}}-\sqrt{4-2\sqrt{3}}\)
\(=\sqrt{3+2.\sqrt{3}.1+1}-\sqrt{3-2.\sqrt{3}.1+1}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\left(\sqrt{3}-1\right)=\sqrt{3}+1-\sqrt{3}+1=2\)
b,\(\sqrt{94+42\sqrt{5}}-\sqrt{94-42\sqrt{5}}\)
\(=\sqrt{49+2.7.3\sqrt{5}+45}-\sqrt{49-2.7.3\sqrt{5}+45}\)
\(=\sqrt{\left(7+3\sqrt{5}\right)^2}-\sqrt{\left(7-3\sqrt{5}\right)^2}\)
\(=7+3\sqrt{5}-\left(7-3\sqrt{5}\right)=6\sqrt{5}\)
9 tháng 8 2018
Bài 2: (chả biết bạn bấm máy hay làm cách nào, nhưng nếu tính tay thì mk hay làm cách này)
a,\(\sqrt{\dfrac{0,144}{10}}=\sqrt{\dfrac{144}{10000}}=\dfrac{\sqrt{144}}{\sqrt{10000}}=\dfrac{12}{100}=\dfrac{3}{25}\)
b,\(\sqrt{\dfrac{1890}{1000}}=\sqrt{\dfrac{189}{100}}=\dfrac{\sqrt{189}}{\sqrt{100}}=\dfrac{\sqrt{9.21}}{10}=\dfrac{3\sqrt{21}}{10}\)
c,\(\dfrac{\sqrt{0,225}}{\sqrt{10}}=\dfrac{\sqrt{225}}{\sqrt{10000}}=\dfrac{15}{100}=\dfrac{3}{20}\)
d,\(\dfrac{\sqrt{8a^5b}}{\sqrt{2ab}}=\sqrt{4a^4b}=2a^2\sqrt{b}\) với a,b > 0
6 tháng 12 2016
mình giải khác @Aliba -@Aliba phân tích thành nhân tử. Mình làm bình thường nhân phân phối
\(\left(1\right)\Leftrightarrow x^2-\left(3y+2\right)x+2y^2+4y=0\)coi như hàm bậc 2 với x giải bình thường
\(\Delta\left(x\right)=\left(3y+2\right)^2-4\left(2y^2+4y\right)=\left(y-2\right)^2\) nhận phân phối ra giản ước là xong
\(\orbr{\begin{cases}x=\frac{3y+2-\left(y-2\right)}{2}=y+2\\x=\frac{3y+2+\left(y-2\right)}{2}=2y\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}y=x-2\\y=\frac{x}{2}\end{cases}}\) thấy y theo x không dúng x thấy y vào (2)
\(\left(2\right)\Leftrightarrow\orbr{\begin{cases}\left(x^2-5\right)^2=2x-2\left(x-2\right)+5\\\left(x^2-5\right)=2x-2.\frac{x}{2}+5\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}\left(x^2-5\right)^2=9\left(3\right)\\\left(x^2-5\right)^2=\left(x+5\right)\left(4\right)\end{cases}}\)
\(\left(3\right)\Leftrightarrow\orbr{\begin{cases}x_{1,2}=+-\sqrt{2}\\x_{3,4}=+-2\sqrt{2}\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}y_{1,2}=+-\sqrt{2}-2\\y_{3,4}=+-2\sqrt{2}-2\end{cases}}\)
\(\left(4\right)\Leftrightarrow x^4-10x^2-x+20=0\)\(\Leftrightarrow\left(x^2-ax+b\right)\left(x^2+ax+c\right)\)đồng nhất hệ số \(\hept{\begin{cases}a=1\\b=-5\\c=-4\end{cases}}\)
\(\left(4\right)\Leftrightarrow\left(x^2-x-5\right)\left(x^2+x-4\right)=0\)
\(\hept{\begin{cases}x^2-x-5=0\\x^2+x-4=0\end{cases}}\)\(\orbr{\begin{cases}\Delta=21\\\Delta=17\end{cases}}\)
\(\orbr{\begin{cases}x_{5,6}=\frac{1+-\sqrt{21}}{2}\\x_{7,8}=\frac{-1+-\sqrt{17}}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}y_{5,6}=\frac{1+-\sqrt{21}}{4}\\y_{7,8}=\frac{-1+-\sqrt{17}}{4}\end{cases}}\)
6 tháng 12 2016
\(\hept{\begin{cases}x^2+2y^2-3xy-2x+4y=0\left(1\right)\\\left(x^2-5\right)^2=2x-2y+5\left(2\right)\end{cases}}\)
Xét \(\left(1\right)\Leftrightarrow\left(x^2-2xy\right)+\left(2y^2-xy\right)+\left(-2x+4y\right)=0\)
\(\Leftrightarrow\left(x-2y\right)\left(x-y-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=2y\\x=2+y\end{cases}}\)
Thế x = 2y vào (2) ta được
\(\left(4y^2-5\right)^2=4y-2y+5\)
\(\Leftrightarrow16y^4-40y^2-2y+20=0\)
\(\Leftrightarrow8y^4-20y^2-y+10=0\)
\(\Leftrightarrow\left(8y^4+4y^3-8y^2\right)+\left(-4y^3-2y^2+4y\right)+\left(-10y^2-5y+10\right)=0\)
\(\Leftrightarrow\left(2y^2+y-2\right)\left(4y^2-2y-5\right)=0\)
Tới đây thì đơn giản rồi. Cái còn lại làm tương tự
MA
2
PT
7 tháng 7 2019
b) \(\sqrt{25a^2}+3a\) \(=5\left|a\right|+3a\)
Vì a > 0 => |a| = a
=> 5|a| + 3a = 5a + 3a = 8a
NT
0
PT
0
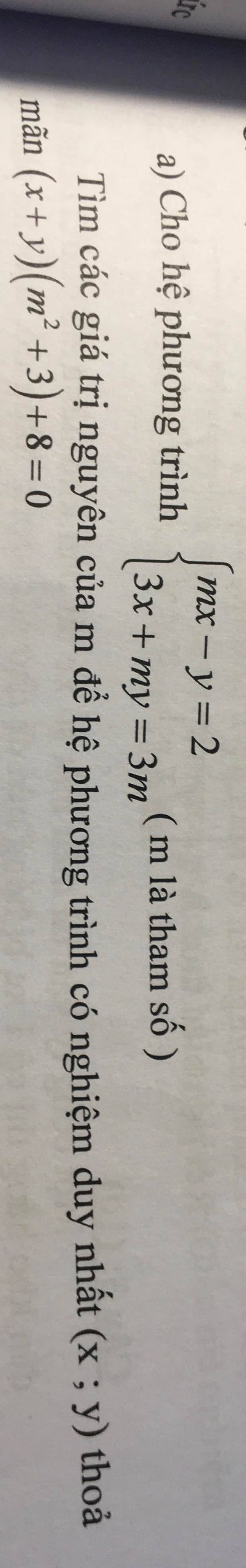
2: Ta có: \(\sqrt{14-8\sqrt{3}}\)
\(=\sqrt{8-2\cdot\sqrt{8}\cdot\sqrt{6}+6}\)
\(=\sqrt{\left(2\sqrt{3}-\sqrt{6}\right)^2}\)
\(=\left|2\sqrt{3}-\sqrt{6}\right|\)
\(=2\sqrt{3}-\sqrt{6}\)
6: Ta có: \(\sqrt{13+4\sqrt{10}}\)
\(=\sqrt{8+2\cdot\sqrt{8}\cdot\sqrt{5}+5}\)
\(=\sqrt{\left(2\sqrt{2}+\sqrt{5}\right)^2}\)
\(=\left|2\sqrt{2}+\sqrt{5}\right|\)
\(=2\sqrt{2}+\sqrt{5}\)
7: Ta có: \(\sqrt{35-12\sqrt{6}}\)
\(=\sqrt{27-2\cdot\sqrt{27}\cdot\sqrt{8}+8}\)
\(=\sqrt{\left(3\sqrt{3}-2\sqrt{2}\right)^2}\)
\(=\left|3\sqrt{3}-2\sqrt{2}\right|\)
\(=3\sqrt{3}-2\sqrt{2}\)