
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

a) x(x + 4) - 3x - 12 = 0
x(x + 4) - 3(x + 4) = 0
(x + 4)(x - 3) = 0
x = -4 hoặc x = 3
b) 2x(x - 4) - x + 4 = 0
2x(x - 4) - (x - 4) = 0
(x - 4)(2x - 1) = 0
x = 4 hoặc x = 1/2
c) 5x(x - 3) - x + 3 = 0
5x(x - 3) - (x - 3) = 0
(x - 3)(5x - 1) = 0
x = 3 hoặc x = 1/5.
a) x(x + 4) - 3x - 12 = 0
x(x + 4) - 3(x + 4) = 0
(x + 4)(x - 3) = 0
x = -4 hoặc x = 3
b) 2x(x - 4) - x + 4 = 0
2x(x - 4) - (x - 4) = 0
(x - 4)(2x - 1) = 0
x = 4 hoặc x = 1/2
c) 5x(x - 3) - x + 3 = 0
5x(x - 3) - (x - 3) = 0
(x - 3)(5x - 1) = 0
x = 3 hoặc x = 1/5.

a: \(\left(2x-1\right)^3-4x^2\left(2x-3\right)=5\)
=>\(8x^3-12x^2+6x-1-8x^3+12x^2=5\)
=>6x-1=5
=>6x=6
=>x=1
b: \(\left(x+1\right)^3-\left(x-1\right)^3-6\left(x-1\right)^2=-10\)
=>\(x^3+3x^2+3x+1-\left(x^3-3x^2+3x-1\right)-6\left(x^2-2x+1\right)=-10\)
=>\(x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6=-10\)
=>12x-4=-10
=>12x=-6
=>\(x=-\frac{6}{12}=-\frac12\)
c: \(\left(x+2\right)^3-x^2\left(x+6\right)=4\)
=>\(x^3+6x^2+12x+8-x^3-6x^2=4\)
=>12x+8=4
=>12x=-4
=>\(x=-\frac{4}{12}=-\frac13\)
d: \(\left(x-2\right)^3-x\left(x+1\right)\left(x-1\right)+6x^2=5\)
=>\(x^3-6x^2+12x-8-x\left(x^2-1\right)+6x^2=5\)
=>\(x^3+12x-8-x^3+x=5\)
=>13x-8=5
=>13x=13
=>x=1
e: \(\left(x-1\right)^3+3\left(x+1\right)^2=\left(x+2\right)\left(x^2-2x+4\right)\)
=>\(x^3-3x^2+3x-1+3\left(x^2+2x+1\right)=x^3+8\)
=>\(-3x^2+3x-1+3x^2+6x+3=8\)
=>9x+2=8
=>9x=6
=>\(x=\frac69=\frac23\)
f: \(\left(x-2\right)^3-\left(x-2\right)\left(x^2+2x+4\right)+6\left(x-2\right)\left(x+2\right)=60\)
=>\(x^3-6x^2+12x-8-\left(x^3-8\right)+6\left(x^2-4\right)=60\)
=>\(-6x^2+12x+6x^2-24=60\)
=>12x-24=60
=>12x=84
=>x=7

a: \(\left(x-3\right)^2-\left(x-3\right)\left(3-x^2\right)=0\)
=>\(\left(x-3\right)\left(x-3-3+x^2\right)=0\)
=>\(\left(x-3\right)\left(x^2+x-6\right)=0\)
=>(x-3)(x+3)(x-2)=0
=>\(\left[\begin{array}{l}x-3=0\\ x+3=0\\ x-2=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=3\\ x=-3\\ x=2\end{array}\right.\)
b: \(4\left(x+1\right)^2+\left(2x-1\right)^2-8\left(x-1\right)\left(x+1\right)=11\)
=>\(4\left(x^2+2x+1\right)+4x^2-4x+1-8\left(x^2-1\right)=11\)
=>\(4x^2+8x+4+4x^2-4x+1-8x^2+8=11\)
=>4x+13=11
=>4x=-2
=>\(x=-\frac24=-\frac12\)
c: \(\left(x-3\right)^2-\left(x+3\right)\left(x-5\right)=3x+4\)
=>\(x^2-6x+9-\left(x^2-5x+3x-15\right)=3x+4\)
=>\(x^2-6x+9-\left(x^2-2x-15\right)=3x+4\)
=>\(x^2-6x+9-x^2+2x+15=3x+4\)
=>-4x+24=3x+4
=>-7x=-20
=>\(x=\frac{20}{7}\)
d: \(3\left(x-5\right)^2+2x\left(x-5\right)=0\)
=>\(\left(x-5\right)\left\lbrack3\left(x-5\right)+2x\right\rbrack=0\)
=>(x-5)(3x-15+2x)=0
=>(x-5)(5x-15)=0
=>5(x-5)(x-3)=0
=>(x-5)(x-3)=0
=>\(\left[\begin{array}{l}x-5=0\\ x-3=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=5\\ x=3\end{array}\right.\)
e: \(\left(2x-1\right)^2-\left(x+3\right)^2=0\)
=>(2x-1-x-3)(2x-1+x+3)=0
=>(x-4)(3x+2)=0
=>\(\left[\begin{array}{l}x-4=0\\ 3x+2=0\end{array}\right.\Rightarrow\left[\begin{array}{l}x=4\\ x=-\frac23\end{array}\right.\)
f: \(4\left(3x+2\right)\left(3x-2\right)-\left(6x+1\right)^2=7\)
=>\(4\left(9x^2-4\right)-36x^2-12x-1=7\)
=>\(36x^2-16-36x^2-12x-1=7\)
=>-12x-17=7
=>-12x=24
=>x=-2
g: \(3\left(2x-1\right)^2-6x\left(2x-3\right)=6\)
=>\(3\left(4x^2-4x+1\right)-6x\left(2x-3\right)=6\)
=>\(12x^2-12x+3-12x^2+18x=6\)
=>6x+3=6
=>6x=3
=>\(x=\frac36=\frac12\)
h: \(\left(2x+3\right)^2-4\left(x-1\right)^2=16\)
=>\(4x^2+12x+9-4\left(x^2-2x+1\right)=16\)
=>\(4x^2+12x+9-4x^2+8x-4=16\)
=>20x+5=16
=>20x=11
=>\(x=\frac{11}{20}\)

\(\left(x^2-2x+3\right)\left(\frac{1}{2x}-5\right)\)
\(=\frac{x^2}{2x}-5x^2-\frac{2x}{2x}+10x+\frac{3}{2x}-15\)
\(=\frac{x^2}{2x}-5x^2-16+10x+\frac{3}{2x}\)
\(=-5x^2+\frac{x^2}{2x}+\frac{20x^2}{2x}+\frac{3}{2x}-16\)
\(=-5x^2+\frac{x^2+20x+3}{2x}-16\)
học tốt
(x^2-2x+3)(1/2x-5)=1/2x^3-5x^2-x^2+10x+3/2x-15=1/2x^3-6x^2+11,5x-15

Lời giải:
Để $x^4+2x^3-ax^2+5x+b$ chia $x^2+x-2$ dư $3x+4$ thì:
$x^4+2x^3-ax^2+5x+b=(x^2+x-2)Q(x)+3x+4$ với $Q(x)$ là đa thức thương.
$\Leftrightarrow x^4+2x^3-ax^2+5x+b=(x-1)(x+2)Q(x)+3x+4$
Cho $x=1$ thì:
$8-a+b=7\Leftrightarrow a-b=1(1)$
Cho $x=-2$ thì:
$-10-4a+b=-2\Leftrightarrow -4a+b=8(2)$
Từ $(1); (2)\Rightarrow a=-3; b=-4$




 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ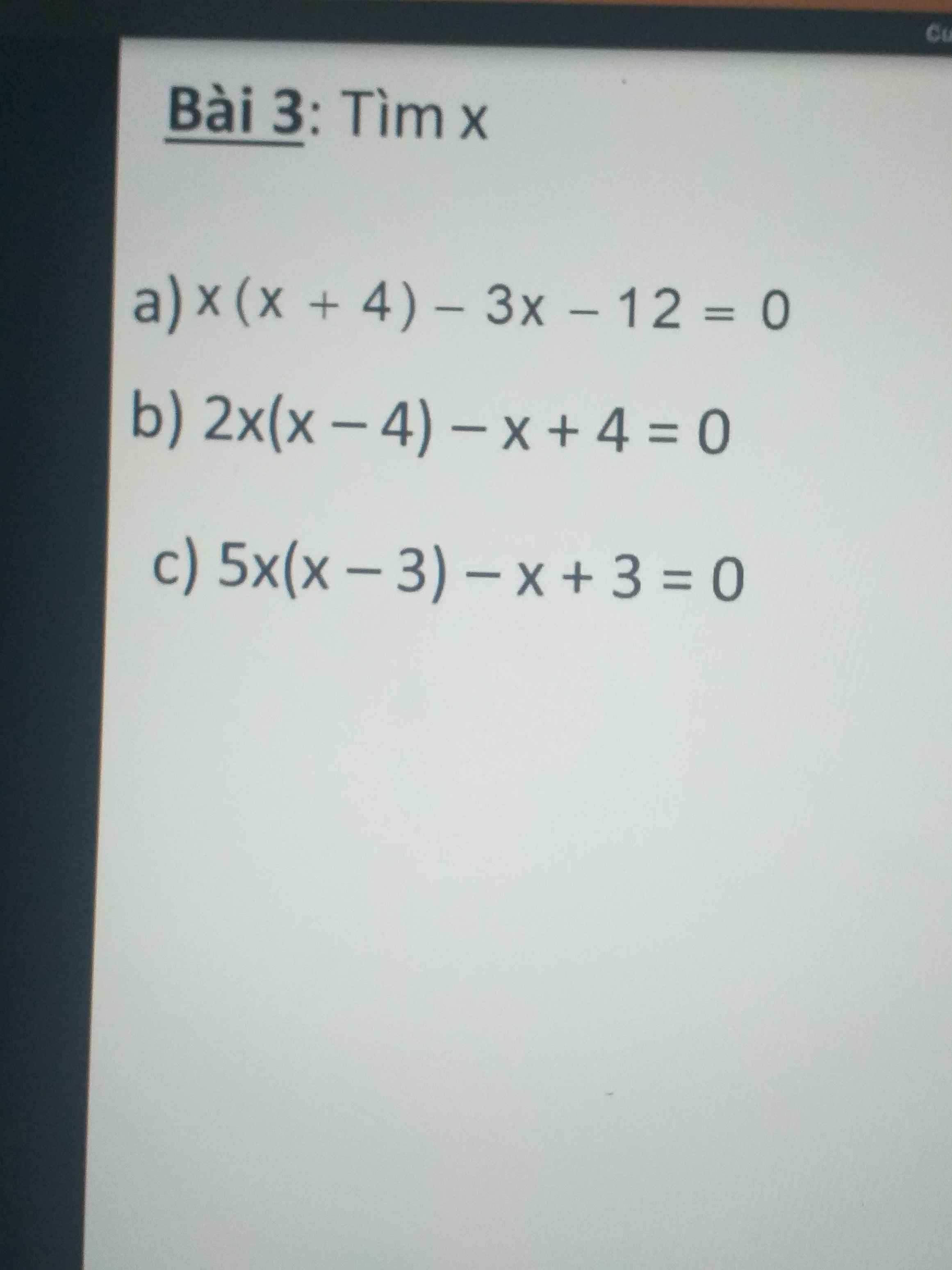


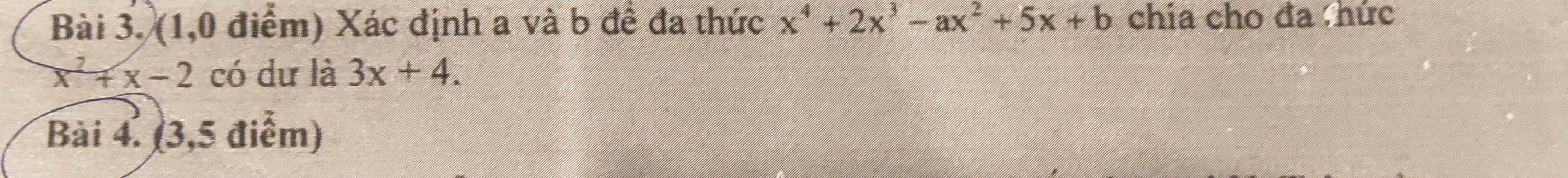 Mọi ng giúp em giải bài này với ạ, em cần gấp.
Mọi ng giúp em giải bài này với ạ, em cần gấp. cd
cd
?/
đâu bài nào