K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
23 tháng 9 2021
j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.
31 tháng 8 2021
cos2x - (2m + 1)cosx + m + 1 = 0
⇔ 2cos2x - (2m + 1).cosx = 0
⇔ \(\left[{}\begin{matrix}cosx=0\left(1\right)\\2cosx=2m+1\left(2\right)\end{matrix}\right.\)
(1) ⇔ \(x=\dfrac{\pi}{2}+k\pi\) với k thuộc Z. Mà \(x\in\left(\dfrac{\pi}{2};2\pi\right)\)
⇒ x = \(\dfrac{3\pi}{2}\)
Như vậy đã có 1 nghiệm trên \(\left(\dfrac{\pi}{2};2\pi\right)\) đó là x = \(\dfrac{3\pi}{2}\). Bây giờ cần tìm m để (2) có 2 nghiệm phân biệt trên \(\left(\dfrac{\pi}{2};2\pi\right)\) và trong 2 nghiệm đó không có nghiệm x = \(\dfrac{3\pi}{2}\). Tức là x = \(\dfrac{3\pi}{2}\) không thỏa mãn (2), tức là
2m + 1 ≠ 0 ⇔ \(m\ne-\dfrac{1}{2}\)
(2) ⇔ \(2.\left(2cos^2\dfrac{x}{2}-1\right)=2m+1\)
⇔ \(4cos^2\dfrac{x}{2}=2m+3\)
Do x \(\in\left(\dfrac{\pi}{2};2\pi\right)\) nên \(\dfrac{x}{2}\in\left(\dfrac{\pi}{4};\pi\right)\) nên cos\(\dfrac{x}{2}\) ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\)
Đặt cos\(\dfrac{x}{2}\) = t ⇒ t ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\). Ta được phương trình : 4t2 = 2m + 3
Cần tìm m để [phương trình được bôi đen] có 2 nghiệm t ∈ \(\left(-1;\dfrac{\sqrt{2}}{2}\right)\)
Dùng hàm số bậc 2 là ra. Nhớ kết hợp điều kiện \(m\ne-\dfrac{1}{2}\)
NT
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)
Hàm chẵn
2.
\(D=R\)
\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)
Hàm không chẵn không lẻ
3.
\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng
\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)
Hàm chẵn
4.
\(D=R\)
\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)
Hàm chẵn
5.
\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng
\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)
Hàm chẵn
HP
8 tháng 10 2021
ĐK: \(x\ne45^o+k.180^o\)
\(tan\left(x+45^o\right)=1+sin2x\)
\(\Leftrightarrow\dfrac{sin\left(x+45^o\right)}{cos\left(x+45^o\right)}=\left(sinx+cosx\right)^2\)
\(\Leftrightarrow\dfrac{sin\left(x+45^o\right)}{cos\left(x+45^o\right)}=2sin^2\left(x+45^o\right)\)
\(\Leftrightarrow sin\left(x+45^o\right)\left[\dfrac{1}{cos\left(x+45^o\right)}-2sin\left(x+45^o\right)\right]=0\)
\(\Leftrightarrow sin\left(x+45^o\right)\left[1-2sin\left(x+45^o\right).cos\left(x+45^o\right)\right]=0\)
\(\Leftrightarrow sin\left(x+45^o\right)\left[1-sin\left(2x+90^o\right)\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+45^o\right)=0\\sin\left(2x+90^o\right)=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+45^o=k.180^o\\2x+90^o=90^o+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-45^o+k.180^o\\x=k.180^o\end{matrix}\right.\)
Đối chiếu điều kiện rồi kết luận.
DN
0
31 tháng 8 2021
cosx = 3m + cos2x + 1
⇔ 2cos2x - cosx + 3m = 0 (1)
Đặt cosx = t. Ta được phương trình : 2t2 - t + 3m = 0.
⇔ 2t2 - t = -3m
(2) là phương trình hoành độ giao điểm của f(t) = 2t2 - t và y = - 3m
Khi x ∈ \(\left(-\pi;-\dfrac{\pi}{2}\right)\) thì t ∈ (- 1 ; 0)
(1) có 1 nghiệm trên \(\left(-\pi;-\dfrac{\pi}{2}\right)\) ⇔ (2) có 1 nghiệm t ∈ (- 1 ; 0)
⇒ f(0) < - 3m < f(-1)
⇒ 0 < - 3m < 3
⇒ - 1 < m < 0 (1)
Khi x ∈ \(\left(-\dfrac{\pi}{2};\dfrac{\pi}{2}\right)\) thì t ∈ (0 ; 1].
(1) có 2 nghiệm trên \(\left(-\dfrac{\pi}{2};\dfrac{\pi}{2}\right)\) khi vầ chỉ khi (2) có 2 nghiệm trên (0 ; 1].
⇒ \(f\left(\dfrac{1}{4}\right)< -3m< f\left(0\right)\)
⇒ \(-\dfrac{1}{8}< -3m< 0\)
⇒ 0 < m < \(\dfrac{1}{24}\) (2)
Từ (1), (2) => Không có m thỏa mãn yêu cầu bài toán
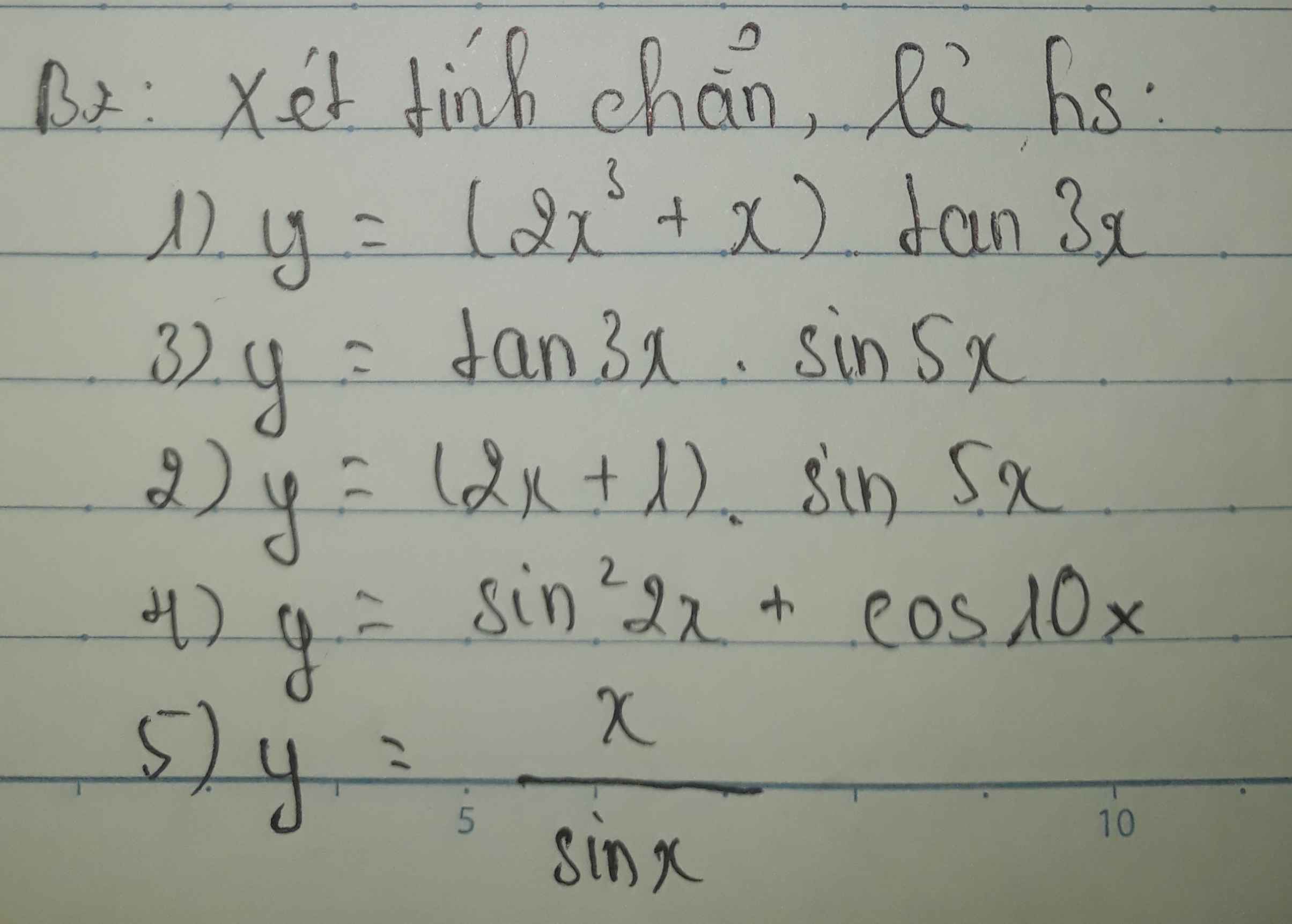
a, \(sinx+cosx=1+sin2x\)
\(\Leftrightarrow sinx+cosx=sin^2x+cos^2x+2sinx.cosx\)
\(\Leftrightarrow sinx+cosx=\left(sinx+cosx\right)^2\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
còn b và c thì s ạ