K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8
\(x+y+z=0\rArr\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2xy+2yz+2zx=0\)
\(\rArr x^2+y^2+z^2+2\left(xy+yz+xz\right)=0\)
\(\rArr x^2+y^2+z^2=0\) (do \(xy+yz+xz=0\) )
\(\rArr x=y=z=0\)
Do đó:
\(\left(x-1\right)^{2023}+y^{2024}+\left(z+1\right)^{2025}=\left(0-1\right)^{2023}+0^{2024}+\left(0+1\right)^{2025}=-1+0+1=0\)
11 tháng 1 2023
a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng
S
subjects
CTVHS
31 tháng 8
theo đề ta có: \(x+y+z=0\Rightarrow\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2\cdot\left(xy+yz+zx\right)=0\)
\(\Rightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\left(1\right)\)
ta co: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
mà x + y + z = 0
\(\Rightarrow x^3+y^3+z^3-3xyz=0\Rightarrow x^3+y^3+z^3=3xyz\left(2\right)\)
a. VT = \(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+x^2z^2\right)\)
ta có: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)+2xyz\cdot\left(x+y+z\right)\)
vì x+y+z=0 nên: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)\)
từ (1) ta có: \(\left(x^2+y^2+z^2\right)^2=\left\lbrack-2\left(xy+yz+zx\right)^{}\right\rbrack^2\) (*)
\(=4\cdot\left(xy+yz+zx\right)^2=4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
ta có: \(4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
mà: \(2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4\)
thay vào (*) ta được:
\(\left(x^2+y^2+z^2\right)^2=\left(x^4+y^4+z^4\right)+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=x^4+y^4+z^4+x^4+y^4+z^4=2\cdot\left(x^4+y^4+z^4\right)=VP\)
⇒ đpcm
b. \(VT=5\cdot\left(x^3+y^3+z^3\right)\left(x^2+y^2+z^2\right)\)
\(=5\cdot\left(3xyz\right)\left(x^2+y^2+z^2\right)\)
\(=15xyz\cdot\left(x^2+y^2+z^2\right)\) (3)
\(x+y+z=0\Rightarrow x+y=-z\)
\(x^5+y^5+z^5=x^5+y^5+\left\lbrack-\left(x+y\right)\right\rbrack^5=x^5+y^5-\left(x+y\right)^5\)
\(=x^5+y^5-\left(x^5+5y^4+10x^3y^2+10x^2y^3+5xy^4+y^5\right)\)
\(=-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=-5xy\left(x^3+2x^2y+2xy^2+y^3\right)\)
\(=-5xy\left\lbrack x^3+y^3+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+y\right)^3-3xy\left(x+Y\right)+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+Y\right)^3-xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left(x+Y\right)\left\lbrack\left(x+y\right)^2-xy\right\rbrack\)
vì x+y=-z nên ta có:
\(x^5+y^5+z^5=-5xy\left(-z\right)\left\lbrack\left(-z\right)^2-xy\right\rbrack=5xyz\left(x^2-zy\right)\)
mặt khác \(x+y=-z\Rightarrow\left(x+y\right)^2=z^2\Rightarrow x^2+y^2+2xy=z^2\)
\(x^2+y^2+z^2=x^2+y^2+\left(x+y\right)^2\)
\(=x^2+y^2+x^2+2xy+y^2=2\cdot\left(x^2+xy+y^2\right)\)
\(z^2-xy=\left(x+y\right)^2-xy=x^2+2xy+y^2-xy=x^2+xy+y^2\)
vậy \(x^5+y^5+z^5=5xyz\cdot\left(x^2+xy+y^2\right)=\frac52xyz\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2\cdot\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
⇒ \(6\cdot\left(x^5+y^5+z^5\right)=15xyz\left(x^2+y^2+z^2\right)\) (4)
từ (3) và (4) ⇒ VT = VP
QT
1
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
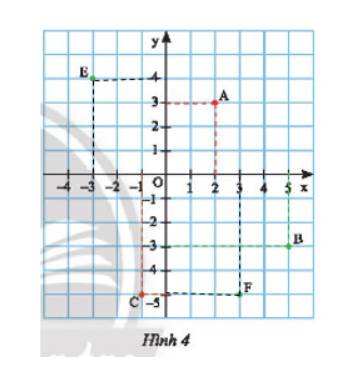
Điểm \(O\) là gốc tọa độ nên \(O\left( {0;0} \right)\)
Từ điểm \(E\) ta vẽ vuông góc với \(Ox;Oy\) cắt \(Ox\) tại – 3 và cắt \(Oy\) tại 4 nên \(E\left( { - 3;4} \right)\).
Từ điểm \(F\) ta vẽ vuông góc với \(Ox;Oy\) cắt \(Ox\) tại 3 và cắt \(Oy\) tại – 5 nên \(E\left( {3; - 5} \right)\).
23 tháng 8
Bài 2:
a: ĐKXĐ: x∉{2;-2}
b: \(A=\frac{3x}{x-2}-\frac{2}{x+2}+\frac{2x-4}{x^2-4}\)
\(=\frac{3x}{x-2}-\frac{2}{x+2}+\frac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\frac{3x}{x-2}-\frac{2}{x+2}+\frac{2}{x+2}=\frac{3x}{x-2}\)
c: Thay x=-5 vào A, ta được:
\(A=\frac{3\cdot\left(-5\right)}{-5-2}=\frac{-15}{-7}=\frac{15}{7}\)
d: Để A nguyên thì 3x⋮x-2
=>3x-6+6⋮x-2
=>6⋮x-2
=>x-2∈{1;-1;2;-2;3;-3;6-6}
=>x∈{1;2;4;0;5;-1;8;-4}
Kết hợp ĐKXĐ, ta được: x∈{1;4;0;5;-1;8;-4}
Bài 1:
a: \(A=x^2+10x+25\)
\(=x^2+2\cdot x\cdot5+5^2=\left(x+5\right)^2\)
b: \(B=x^2-y^2+8x-8y\)
=(x-y)(x+y)+8(x-y)
=(x-y)(x+y+8)
c: \(C=x^2+4x-5\)
\(=x^2+5x-x-5\)
=x(x+5)-(x+5)
=(x+5)(x-1)
S
subjects
CTVHS
31 tháng 8
theo đề ta có: \(x+y+z=0\Rightarrow\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2+2\cdot\left(xy+yz+zx\right)=0\)
\(\Rightarrow x^2+y^2+z^2=-2\left(xy+yz+xz\right)\left(1\right)\)
ta co: \(x^3+y^3+z^3-3xyz=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-xz\right)\)
mà x + y + z = 0
\(\Rightarrow x^3+y^3+z^3-3xyz=0\Rightarrow x^3+y^3+z^3=3xyz\left(2\right)\)
a. VT = \(\left(x^2+y^2+z^2\right)^2=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+x^2z^2\right)\)
ta có: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)+2xyz\cdot\left(x+y+z\right)\)
vì x+y+z=0 nên: \(\left(xy+yz+zx\right)^2=\left(x^2y^2+y^2z^2+x^2z^2\right)\)
từ (1) ta có: \(\left(x^2+y^2+z^2\right)^2=\left\lbrack-2\left(xy+yz+zx\right)^{}\right\rbrack^2\) (*)
\(=4\cdot\left(xy+yz+zx\right)^2=4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
ta có: \(4\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
mà: \(2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)=x^4+y^4+z^4\)
thay vào (*) ta được:
\(\left(x^2+y^2+z^2\right)^2=\left(x^4+y^4+z^4\right)+2\cdot\left(x^2y^2+y^2z^2+z^2x^2\right)\)
\(=x^4+y^4+z^4+x^4+y^4+z^4=2\cdot\left(x^4+y^4+z^4\right)=VP\)
⇒ đpcm
b. \(VT=5\cdot\left(x^3+y^3+z^3\right)\left(x^2+y^2+z^2\right)\)
\(=5\cdot\left(3xyz\right)\left(x^2+y^2+z^2\right)\)
\(=15xyz\cdot\left(x^2+y^2+z^2\right)\) (3)
\(x+y+z=0\Rightarrow x+y=-z\)
\(x^5+y^5+z^5=x^5+y^5+\left\lbrack-\left(x+y\right)\right\rbrack^5=x^5+y^5-\left(x+y\right)^5\)
\(=x^5+y^5-\left(x^5+5y^4+10x^3y^2+10x^2y^3+5xy^4+y^5\right)\)
\(=-5x^4y-10x^3y^2-10x^2y^3-5xy^4\)
\(=-5xy\left(x^3+2x^2y+2xy^2+y^3\right)\)
\(=-5xy\left\lbrack x^3+y^3+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+y\right)^3-3xy\left(x+Y\right)+2xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left\lbrack\left(x+Y\right)^3-xy\left(x+y\right)\right\rbrack\)
\(=-5xy\left(x+Y\right)\left\lbrack\left(x+y\right)^2-xy\right\rbrack\)
vì x+y=-z nên ta có:
\(x^5+y^5+z^5=-5xy\left(-z\right)\left\lbrack\left(-z\right)^2-xy\right\rbrack=5xyz\left(x^2-zy\right)\)
mặt khác \(x+y=-z\Rightarrow\left(x+y\right)^2=z^2\Rightarrow x^2+y^2+2xy=z^2\)
\(x^2+y^2+z^2=x^2+y^2+\left(x+y\right)^2\)
\(=x^2+y^2+x^2+2xy+y^2=2\cdot\left(x^2+xy+y^2\right)\)
\(z^2-xy=\left(x+y\right)^2-xy=x^2+2xy+y^2-xy=x^2+xy+y^2\)
vậy \(x^5+y^5+z^5=5xyz\cdot\left(x^2+xy+y^2\right)=\frac52xyz\left(x^2+y^2+z^2\right)\)
\(\Rightarrow2\cdot\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
⇒ \(6\cdot\left(x^5+y^5+z^5\right)=15xyz\left(x^2+y^2+z^2\right)\) (4)
từ (3) và (4) ⇒ VT = VP
c: Xét ΔANB có
EM//NB
E là trung điểm của AB
=>M là trung điểm của AN
=>AM=MN
Xét ΔDMC có
F là trung điểm của CD
FN//DM
=>N là trung điểm của CM
=>CN=NM=AM
AM+MO=AO
CN+NO=CO
mà AO=CO và AM=Cn
nên MO=NO
=>O là trung điểm của MN
=>M đối xứng N qua O