
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2, \(\widehat{ABC} + \widehat{BCA} = \widehat{BAC} = 90^0 ⇒ \widehat{BCA} = 90^0 - \widehat{ABC}\)
\(\widehat{ABC} +\widehat{ BAH} = \widehat{BAC} =90^0⇒\widehat{BAH} = 90^0 - \widehat{ABC}\)
\(\widehat{BCA} = \widehat{BAH}\)
XÉT \(\bigtriangleup\)HBA và\(\bigtriangleup\) HAC có :
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{BCA}=\widehat{BAH}\)
⇒ \(\bigtriangleup\)HBA ∼ \(\bigtriangleup\) HAC
b, Áp dụng hệ thức \(b^2=a.b'\) vào \(\bigtriangleup{ABC}\) vuông tại A , ta có :
\(AC^2=BC.CH\) (đpcm)
c, Áp dụng hệ thức \(h^2=b'.c'\) vào \(\bigtriangleup{ABC}\) vuông tại A, ta có :
\(AH^2=BH.CH\) (đpcm)



\(\left(\frac{1}{2}xy-1\right).\left(x^3-2x-6\right)=\frac{1}{2}xy.\left(x^3-2x-6\right)+\left(-1\right).\left(x^3-2x-6\right)\)
= \(\frac{1}{2}xy.x^3+\frac{1}{2}xy.\left(-2x\right)+\frac{1}{2xy}.\left(-6\right)+\left(-1\right).x^3+\left(-1\right).\left(-2x\right)+\left(-1\right).\left(-6\right)\)
= \(\frac{1}{2}x^{\left(1+3\right)}y-x^{\left(1+1\right)}y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^2y-3xy-x^3+2x+6\)
= \(\frac{1}{2}x^4y-x^3-x^2y-3xy+2x+6\)
Chúc bạn học tốt !!!
Bài làm
Ta có: ( xy - 1 )( x3 - 2x - 6 )
= ( xy . x3 ) + [ xy . ( -2x ) ] + [ xy . ( - 6 ) ] + [ ( -1 ) . x3 ] + [ ( -1 ) . ( -2x ) ] + [ ( -1 ) . ( -6 ) ] ( * chỗ này nếu thầnh thạo phép nnhân đa thức r thì k cần pk ghi đâu )
= x4y - 2x2y - 6xy - x3 + 2x + 6
# Học tốt #

-
Dùng định nghĩa hai phân thức bằng nhau chứng tỏ rằng:
- Chứng Tỏ Rằng J Hả Bạn ??????
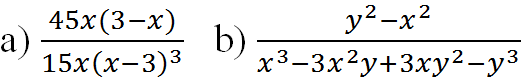
 xy – 1 với đa thức x3 – 2x – 6.
xy – 1 với đa thức x3 – 2x – 6.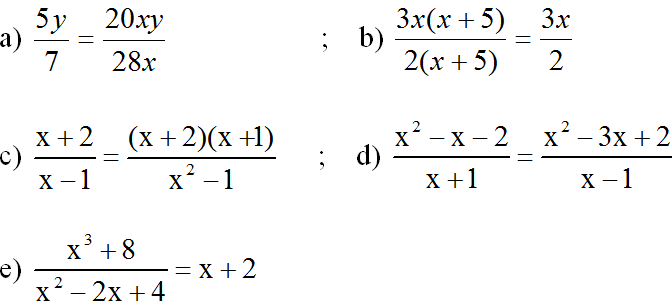
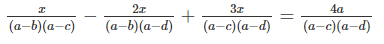
Đề bài
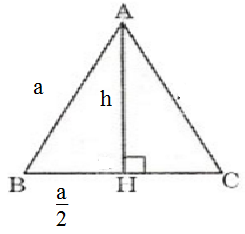
Cho hình thang ABCD (AB, CD là hai đáy). Gọi M, N, P, Q lần lượt là trung điểmcủa AB, AC, CD, BD.
a) M, N lần lượt là trung điểm của AB và BC (gt);
⇒MN⇒MN là đường trung bình của tam giác ABC
⇒MN//AC⇒MN//AC và ..
Q, P lần lượt là trung điểm của AD và CD (gt);
⇒QP⇒QP là đường trung bình của tam giác ADC
⇒QP//AC⇒QP//AC và QP=12AC(2)QP=12AC(2)
Từ (1) và (2) ⇒MN//QP⇒MN//QP và MN=QPMN=QP
Vậy tư giác MNPQ là hình bình hành.
b) Ta có tứ giác MNPQ là hình bình hành.
MN // AC, MN=AC2MN=AC2 (MN là đường trung bình của tam giác ABC)
MQ // BD, MQ=BD2MQ=BD2 (MQ là đường trung bình của tam giác ABD)
* Tứ giác MNPQ là hình thoi ⇔⇔ Hình bình hành MNPQ có MN=MQ⇔AC=BDMN=MQ⇔AC=BD
Vậy hình thanh ABCD cần có thêm điều kiện AC=BDAC=BD để tứ giác MNPQ là hình thoi.
* Tứ giác MNPQ là hình chữ nhật ⇔⇔ Hình bình hành MNPQ có ˆNMQ=900NMQ^=900
⇒MN⊥MQ⇔MQ⊥AC⇔AC⊥BD⇒MN⊥MQ⇔MQ⊥AC⇔AC⊥BD
Vậy hình thang ABCD cần có thêm điều kiện AC⊥BDAC⊥BD để tứ giác MNPQ là hình chữ nhật.
* Tứ giác MNPQ là hình vuông ⇔⇔ Hình thoi MNPQ có ˆNMQ=900⇔AC=BDNMQ^=900⇔AC=BD và AC⊥BDAC⊥BD
Vậy hình thang ABCD cần thêm điều kiện AC=BD,AC⊥BDAC=BD,AC⊥BD để tứ giác MNPQ là hình vuông.
Xem thêm tại: https://loigiaihay.com/bai-tap-2-trang-140-tai-lieu-day-hoc-toan-8-tap-1-c242a43131.html#ixzz5Y0XJF4SV
đây là bài làm mik tham khảo thôi nha