HC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 1 2024
M A O B E F H K P Q
a/
Ta có
AE = HE; BF = HF (2 tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì khoảng cách từ điểm đó đến 2 tiếp điểm bằng nhau)
=> AE + BF = HE + HF = EF (dpcm)
b/ Gọi P; K; Q lần lượt là giao của OE; OM; OF với (O)
Ta có
sđ cung PA = sđ cung PH (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
sđ cung QB = sđ cung QH (lý do như trên)
=> sđ cung PH + sđ cung QH = sđ cung PA + sđ cung QB
=> sđ cung APH = sđ cung BQH
Mà sđ cung APH + sđ cung BQH = sđ cung AKB
=> sđ cung APH = sđ cung BQH = \(\dfrac{sđcungAKB}{2}\) (1)
Ta có
sđ cung KA = sđ cung KB (Hai tiếp tuyến cùng xp từ 1 điểm ngoài hình tròn thì đường nối điểm đó với tâm chia đôi cung chắn bởi 2 tiếp điểm)
Mà sđ cung KA + sđ cung KB = sđ cung AKB
=> sđ cung KA = sđ cung KB = \(\dfrac{sđcungAKB}{2}\) (2)
Ta có
\(sđ\widehat{MOA}=sđcungKA=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (3)
\(sđ\widehat{FOE}=sđcungPHQ=sđcungPH+sđcungQH=\dfrac{sđcungAKB}{2}\) (góc ở tâm đường tròn) (4)
Từ (1) (2) (3) (4) \(\Rightarrow\widehat{MOA}=\widehat{FOE}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2024
ĐKXĐ: \(x+2y\ne0\)
\(\left\{{}\begin{matrix}x-\dfrac{1}{x+2y}=\dfrac{7}{4}\\-\dfrac{5}{2}x+2+\dfrac{4}{x+2y}=-2\end{matrix}\right.\)
Đặt \(\dfrac{1}{x+2y}=z\) ta được hệ:
\(\left\{{}\begin{matrix}x-z=\dfrac{7}{4}\\-\dfrac{5}{2}x+4z=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\z=\dfrac{1}{4}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{x+2y}=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\x+2y=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
PD
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2024
Gọi số xe dự định tham gia chở hàng là x (xe) với x>4, x nguyên dương
Mỗi xe dự định chở khối lượng hàng là: \(\dfrac{20}{x}\) (tấn)
Số xe thực tế tham gia chở hàng là: \(x-4\) (xe)
Thực tế mỗi xe phải chở số hàng là: \(\dfrac{20}{x-4}\) (tấn)
Do thực tế mỗi xe phải chở nhiều hơn dự định là 5/6 tấn hàng nên ta có pt:
\(\dfrac{20}{x-4}-\dfrac{20}{x}=\dfrac{5}{6}\)
\(\Rightarrow24x-24\left(x-4\right)=x\left(x-4\right)\)
\(\Leftrightarrow x^2-4x-96=0\)
\(\Rightarrow\left[{}\begin{matrix}x=12\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy thực tế có \(12-4=8\) xe tham gia vận chuyển
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 12 2022
Mình không thấy câu nào cả thì giúp kiểu gì lỗi ảnh hay sao ý
A
16 tháng 8
a) Rút gọn A rồi tìm \(x\) để \(A\) đạt GTNN
Nhận xét:
\(x^{2} - 8 x + 16 = \left(\right. x - 4 \left.\right)^{2} \Rightarrow \sqrt{x^{2} - 8 x + 16} = \mid x - 4 \mid = x - 4 \left(\right. v \overset{ˋ}{\imath} x > 4 \left.\right)\)
Xét biểu thức trong ngoặc:
\(\sqrt{x + 4 \sqrt{x - 4}} = \sqrt{\left(\right. \sqrt{x - 4} + 2 \left.\right)^{2}} , \sqrt{x - 4 \sqrt{x - 4}} = \sqrt{\left(\right. \sqrt{x - 4} - 2 \left.\right)^{2}}\)
⇒ Với \(x > 4\), ta có:
\(\sqrt{x + 4 \sqrt{x - 4}} = \sqrt{x - 4} + 2 , \sqrt{x - 4 \sqrt{x - 4}} = \mid \sqrt{x - 4} - 2 \mid = \sqrt{x - 4} - 2 \left(\right. v \overset{ˋ}{\imath} \sqrt{x - 4} > 2 \left.\right)\)
⇒ Tổng:
\(\sqrt{x + 4 \sqrt{x - 4}} + \sqrt{x - 4 \sqrt{x - 4}} = \left(\right. \sqrt{x - 4} + 2 \left.\right) + \left(\right. \sqrt{x - 4} - 2 \left.\right) = 2 \sqrt{x - 4}\)
Do đó:
\(A = \frac{x \cdot 2 \sqrt{x - 4}}{x - 4} = \frac{2 x \sqrt{x - 4}}{x - 4} = \frac{2 x}{\sqrt{x - 4}}\)
Xét hàm \(A \left(\right. x \left.\right) = \frac{2 x}{\sqrt{x - 4}} , \&\text{nbsp}; x > 4\)
Đặt \(t = \sqrt{x - 4} > 0 \Rightarrow x = t^{2} + 4\)
\(A = \frac{2 \left(\right. t^{2} + 4 \left.\right)}{t} = 2 t + \frac{8}{t}\)
Tìm GTNN của hàm \(f \left(\right. t \left.\right) = 2 t + \frac{8}{t} , \&\text{nbsp}; t > 0\)
Áp dụng BĐT AM-GM:
\(2 t + \frac{8}{t} \geq 2 \sqrt{2 t \cdot \frac{8}{t}} = 2 \sqrt{16} = 8\)
Dấu “=” xảy ra khi \(2t=\frac{8}{t}\Rightarrow t^2=4\Rightarrow t=2\Rightarrow x=t^2+4=8\)
P
Phong
CTVHS
15 tháng 10 2023
b) \(\sqrt{x^2}=\left|-8\right|\)
\(\Rightarrow\left|x\right|=8\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)
d) \(\sqrt{9x^2}=\left|-12\right|\)
\(\Rightarrow\sqrt{\left(3x\right)^2}=12\)
\(\Rightarrow\left|3x\right|=12\)
\(\Rightarrow\left[{}\begin{matrix}3x=12\\3x=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{12}{3}\\x=-\dfrac{12}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-4\end{matrix}\right.\)
17 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}2x-3>=0\\x+1>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{3}{2}\\x>=-1\end{matrix}\right.\)
=>\(x>=\dfrac{3}{2}\)
\(\sqrt{2x-3}-\sqrt{x+1}=x-4\)
=>\(\dfrac{2x-3-x-1}{\sqrt{2x-3}+\sqrt{x+1}}-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt{2x-3}+\sqrt{x+1}}-1\right)=0\)
=>x-4=0
=>x=4(nhận)
14 giờ trước (13:28)
a: \(\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)\cdot\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{x}+\frac{1}{y}\)
\(=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\cdot\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{x+y}{xy}\)
\(=\frac{2}{\sqrt{xy}}+\frac{x+y}{xy}=\frac{x+y+2\sqrt{xy}}{xy}=\frac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy}\)
\(\frac{\sqrt{x^3}+x\cdot\sqrt{y}+y\cdot\sqrt{x}+\sqrt{y^3}}{\sqrt{x^3y}+\sqrt{xy^3}}\)
\(=\frac{\left(x\cdot\sqrt{x}+x\cdot\sqrt{y}+y\cdot\sqrt{x}+y\cdot\sqrt{y}\right)}{x\cdot\sqrt{xy}+y\cdot\sqrt{xy}}=\frac{\left(x+y\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{xy}\left(x+y\right)}=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\)
\(P=\left\lbrack\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)\cdot\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{x}+\frac{1}{y}\right\rbrack:\left(\frac{\sqrt{x^3}+x\cdot\sqrt{y}+y\cdot\sqrt{x}+\sqrt{y^3}}{\sqrt{x^3y}+\sqrt{xy^3}}\right)\)
\(=\frac{\left(\sqrt{x}+\sqrt{y}\right)^2}{xy}:\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}=\frac{\sqrt{x}+\sqrt{y}}{\sqrt{xy}}\)
TT
Trần Thị Thu
VIP
14 giờ trước (13:34)
nhu nay bn nhe a: \(\left(\right. \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} \left.\right) \cdot \frac{2}{\sqrt{x} + \sqrt{y}} + \frac{1}{x} + \frac{1}{y}\)
\(= \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y}} \cdot \frac{2}{\sqrt{x} + \sqrt{y}} + \frac{x + y}{x y}\)
\(= \frac{2}{\sqrt{x y}} + \frac{x + y}{x y} = \frac{x + y + 2 \sqrt{x y}}{x y} = \frac{\left(\left(\right. \sqrt{x} + \sqrt{y} \left.\right)\right)^{2}}{x y}\)
\(\frac{\sqrt{x^{3}} + x \cdot \sqrt{y} + y \cdot \sqrt{x} + \sqrt{y^{3}}}{\sqrt{x^{3} y} + \sqrt{x y^{3}}}\)
\(= \frac{\left(\right. x \cdot \sqrt{x} + x \cdot \sqrt{y} + y \cdot \sqrt{x} + y \cdot \sqrt{y} \left.\right)}{x \cdot \sqrt{x y} + y \cdot \sqrt{x y}} = \frac{\left(\right. x + y \left.\right) \left(\right. \sqrt{x} + \sqrt{y} \left.\right)}{\sqrt{x y} \left(\right. x + y \left.\right)} = \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y}}\)
\(P = \left[\right. \left(\right. \frac{1}{\sqrt{x}} + \frac{1}{\sqrt{y}} \left.\right) \cdot \frac{2}{\sqrt{x} + \sqrt{y}} + \frac{1}{x} + \frac{1}{y} \left]\right. : \left(\right. \frac{\sqrt{x^{3}} + x \cdot \sqrt{y} + y \cdot \sqrt{x} + \sqrt{y^{3}}}{\sqrt{x^{3} y} + \sqrt{x y^{3}}} \left.\right)\)
\(= \frac{\left(\left(\right. \sqrt{x} + \sqrt{y} \left.\right)\right)^{2}}{x y} : \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y}} = \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y}}\)
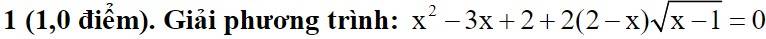
\(x^2+3x+2+2\left(2-x\right)\sqrt{x-1}=0\left(x\ge1\right)\)
\(\Leftrightarrow x^2-x-2x+2-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow x\left(x-1\right)-2\left(x-1\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)-2\left(x-2\right)\sqrt{x-1}=0\)
\(\Leftrightarrow\left(x-2\right)\sqrt{x-1}\left(\sqrt{x-1}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\\sqrt{x-1}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x-1=0\\\sqrt{x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=1\left(tm\right)\\x-1=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\\x=5\end{matrix}\right.\left(tm\right)\)
Vậy: \(x\in\left\{1;2;5\right\}\)