Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đặt phương trình parabol là \(\left( P \right):h = a{t^2} + bt + c\)
Ta có quả bóng được đá lên từ điểm A(0; 0,2) nên \(0,2 = c\)
Ta có quả bóng đạt độ cao 8,5 m sau 1 giây có nghĩa là tại t=1 thì h=8,5. Khi đó
\(8,5 = a + b+0,2 \Leftrightarrow a+b = 8,3\) (1)
Ta có quả bóng đạt độ cao 6 m sau 2 giây có nghĩa là tại t=2 thì h=6.
=> \(6 = a{.2^2} + b.2+0,2 \)\( \Leftrightarrow 2a + b = 2,9\) (2)
Từ (1) và (2) ta được hệ \(\left\{ \begin{array}{l}a + b = 8,3\\2a + b = 2,9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 5,4\\b = 13,7 \end{array} \right.\)
Vậy \(\left( P \right):h = - 5,4{t^2} + 13,7t+0,2\)
b) Để quả bóng không chạm đất thì \(h > 0\)
\(\Leftrightarrow - 5,4{t^2} + 13,7t+0,2 > 0\)
PT \(- 5,4{t^2} + 13,7t+0,2 = 0\) có hai nghiệm xấp xỉ là \(t_1 = -0,0145\) và \(t_2 = 2,55\)
Sử dụng định lí về dấu, ta có \(h>0\) khi \(t_1 <t< t_2\) suy ra \(0<t<2,55\) (vì t>0)
Vậy trong khoảng thời gian từ lúc đá đến thời gian \(t = 2,55\) thì quả bóng chưa chạm đất.

Gọi phương trình chuyển động của quả bóng có dạng \(y=at^2+bt+c\)
\(t=0;y=1\Rightarrow c=1\)
\(t=1;y=7\Rightarrow a+b+1=7\Rightarrow a+b=6\)
\(t=2;y=9\Rightarrow4a+2b+1=9\Rightarrow2a+b=4\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\end{matrix}\right.\)
\(\Rightarrow y=-2t^2+8t+1\)
Các thời điểm mà độ cao quả bóng đạt 7m là:
\(-2t^2+8t+1=7\Rightarrow2t^2-8t+6=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=3\end{matrix}\right.\)
Vậy quả bóng đạt độ cao lớn hơn 7m trong khoảng thời gian 2s (từ giây thứ 1 đến giây thứ 3)
Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9 m sau 2 giây. Trong khoảng thời gian bao lâu thì độ cao quả bóng nhỏ hơn 7 m.

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:
\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow - 4,9{t^2} + 30t - 38 > 0\end{array}\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 30t - 38\) có \(\Delta = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
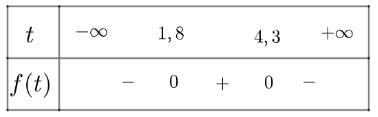
Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m
Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.

Để quả bóng có thể ném được qua lưới cao 2 m thì \(y = f\left( x \right) = - 0,03{x^2} + 0,4x + 1,5 > 2\)
\( \Rightarrow f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5 > 0\)
Xét tam thức \(f\left( x \right) = - 0,03{x^2} + 0,4x - 0,5\) có \(\Delta = 0,1 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,4;{x_2} \simeq 11,9\) và có \(a = - 0,03 < 0\)
Ta có bảng xét dấu như sau
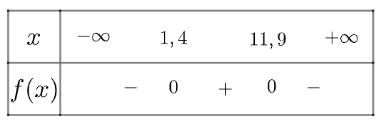
Vậy để quả bóng có thể ném được qua lưới cao 2 m, người ta phải đứng cách lưới từ 1,4 cho đến 11,9 mét

Thay t=0 và h=1,5 vào \(h=a\cdot t^2+bt+c\), ta được:
\(a\cdot0^2+b\cdot0+c=1,5\)
=>c=1,5
=>\(h=at^2+bt+1,5\)(1)
Thay t=2 và h=5 vào (1), ta được:
\(a\cdot2^2+b\cdot2+1,5=5\)
=>4a+2b=3,5(2)
Thay t=4 và h=4,5 vào (1), ta được:
\(a\cdot4^2+b\cdot4+1,5=4,5\)
=>16a+4b=3(3)
Từ (2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+2b=3,5\\16a+4b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8a+4b=7\\16a+4b=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8a+4b-16a-4b=7-3\\4a+2b=3,5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-8a=4\\2b=3,5-4a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-0,5\\2b=3,5-4\cdot\left(-0,5\right)=5,5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-0,5\\b=2,75\end{matrix}\right.\)
Vậy: \(h=-0,5t^2+2,75t+1,5\)
Thay t=5,5 vào h, ta được:
\(h=-0,5\cdot5,5^2+2,75\cdot5,5+1,5=1,5\left(mét\right)\)