Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\Leftrightarrow3^x\cdot3+2x\cdot3^x-18x-27=0\)
\(\Leftrightarrow3^x\left(2x+3\right)-9\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x+3\right)\left(3^x-9\right)=0\)
=>x=2 hoặc x=-3/2
b: \(\Leftrightarrow\left|2x+5\right|\cdot\dfrac{1}{2}-\dfrac{5}{4}\cdot2\cdot\left|2x+5\right|+\dfrac{7}{3}\cdot4\cdot\left|2x+5\right|=\dfrac{1}{6}\)
\(\Leftrightarrow\left|2x+5\right|=\dfrac{1}{44}\)
=>2x+5=1/44 hoặc 2x+1=-1/44
=>x=-219/88 hoặc x=-221/88

\(A=\dfrac{1-\left|8x-\dfrac{2}{3}\right|}{2}\)
\(\left|8x-\dfrac{2}{3}\right|\ge0\forall x\)
\(\Rightarrow1-\left|8x-\dfrac{2}{3}\right|\le1\)
\(MAX_A\Rightarrow MAX_{1-\left|8x-\dfrac{2}{3}\right|}\)
\(MAX_{1-\left|8x-\dfrac{2}{3}\right|}=1\)
Xảy ra khi và chỉ khi:
\(\left|8x-\dfrac{2}{3}\right|=0\Rightarrow8x=\dfrac{2}{3}\Rightarrow x=\dfrac{1}{12}\)
\(\Rightarrow MAX_A=\dfrac{1}{12}\) khi \(x=\dfrac{1}{12}\)
\(B=5-\left|\dfrac{3}{5}-2x\right|+2\)
\(B=7-\left|\dfrac{3}{5}-2x\right|\)
\(\left|\dfrac{3}{5}-2x\right|\ge0\forall x\)
\(\Rightarrow7-\left|\dfrac{3}{5}-2x\right|\le7\)
(ko tìm được MIN đâu nhé)
Dấu "=" xảy ra khi:
\(\left|\dfrac{3}{5}-2x\right|=0\Rightarrow\dfrac{3}{5}=2x\Rightarrow x=\dfrac{3}{10}\)
\(\Rightarrow MAX_B=7\) khi \(x=\dfrac{3}{10}\)
a) ta có : \(\left|8x-\dfrac{2}{3}\right|\ge0\Rightarrow1-\left|8x-\dfrac{2}{3}\right|\le1\Rightarrow\dfrac{1-\left|8x-\dfrac{2}{3}\right|}{2}\le\dfrac{1}{2}\) Vậy GTLN của A=\(\dfrac{1}{2}\) khi và chỉ khi x=\(\dfrac{1}{12}\)
b) Giải tương tự câu a

a: =>5x+1=6/7 hoặc 5x+1=-6/7
=>5x=-1/7 hoặc 5x=-13/7
=>x=-1/35 hoặc x=-13/35
b: =>x-2/9=4/9
=>x=6/9=2/3
c: =>8x+1=5
=>8x=4
hay x=1/2

b) \(\left(x-\dfrac{2}{9}\right)^3=\left(\dfrac{2}{3}\right)^6\)
\(\Rightarrow\left(x-\dfrac{2}{9}\right)^3=\left[\left(\dfrac{2}{3}\right)^2\right]^3=\left(\dfrac{4}{9}\right)^3\)
\(\Rightarrow x-\dfrac{2}{9}=\dfrac{4}{9}\)
\(\Rightarrow x=\dfrac{2}{3}\)

1) a)
=\(\left(4-1+8\right)x^2=11x^2\)
b) =\(\left(\dfrac{1}{2}-\dfrac{3}{4}+1\right)x^2y^2=\dfrac{3}{4}x^2y^2\)
c) =(3-7+4-6)y=5y 2) a) ...=\(\left[\left(\dfrac{-2}{3}y^3\right)-\dfrac{1}{2}y^3\right]+3y^2-y^2\\ =\left[\left(\dfrac{-2}{3}-\dfrac{1}{2}\right)y^3\right]+\left(3-1\right)y^2=\dfrac{-7}{6}y^3+2y^2\) b) ...=\(\left(5x^3-x^3\right)-\left(3x^2+4x^2\right)+\left(x-x\right)=4x^3-7x^2\) 3) a)A=\(\left(5.\dfrac{1}{2}\right).\left(x.x^2.x\right)\left(y^2.y^2\right)=\dfrac{5}{2}x^4y^4\) b)Vậy Đơn thức A có bậc 8; hệ số là \(\dfrac{5}{2}\); phần biến là \(x^4y^4\) c)Khi x=1;y=-1 thì A=\(\dfrac{5}{2}.1^4.\left(-1\right)^4=\dfrac{5}{2}\)

a) \(\left(8x-3\right)\left(3x+2\right)-\left(4x+7\right)\left(x+4\right)=\left(2x+1\right)\left(5x-1\right)-33\)
\(20x^2-16x-34=10x^2+3x-34\)
\(10x^2-19x=0\)
\(x\left(10x-19\right)=0\)
\(\Leftrightarrow x=0\)
hoặc \(10x-19=0\)
\(\Leftrightarrow x=\dfrac{19}{10}\)
Vạy ..............
b) \(\dfrac{x-1}{x+5}=\dfrac{6}{7}\)
\(\Leftrightarrow1-\dfrac{x-1}{x+5}=1-\dfrac{6}{7}\)
\(\Leftrightarrow\dfrac{x+5}{x+5}-\dfrac{x-1}{x+5}=\dfrac{7}{7}-\dfrac{6}{7}\)
\(\Leftrightarrow\dfrac{\left(x+5\right)-\left(x-1\right)}{x+5}=\dfrac{1}{7}\)
\(\Leftrightarrow\dfrac{x+5-x+1}{x+5}=\dfrac{1}{7}\)
\(\Leftrightarrow\dfrac{\left(x-x\right)+\left(5+1\right)}{x+5}=\dfrac{1}{7}\)
\(\Leftrightarrow\dfrac{6}{x+5}=\dfrac{1}{7}\)
\(\Leftrightarrow x+5=42\)
\(\Leftrightarrow x=37\)

Ta có: P(x) = -5x3 - 1313 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 - 2323.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
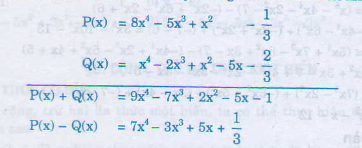 .
.
Ta có: P(x) = -5x3 – 1/3 + 8x4 + x2 và Q(x) = x2 – 5x – 2x3 + x4 – 2/3.
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:

ĐKXĐ: \(x\ne\pm\dfrac{1}{2}\)
\(\dfrac{8x^2}{3\left(1-4x^2\right)}=\dfrac{2x}{6x-3}-\dfrac{1+8x}{4+8x}\)
\(\Leftrightarrow\dfrac{-8x^2}{3\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x}{3\left(2x-1\right)}-\dfrac{1+8x}{4\left(2x+1\right)}\)
\(\Leftrightarrow\dfrac{-32x^2}{12\left(2x-1\right)\left(2x+1\right)}=\dfrac{8x\left(2x+1\right)}{12\left(2x-1\right)\left(2x+1\right)}-\dfrac{3\left(1+8x\right)\left(2x-1\right)}{12\left(2x-1\right)\left(2x+1\right)}\)
\(\Rightarrow-32x^2=16x^2+8x-3\left(16x^2-6x-1\right)\)
\(\Leftrightarrow-32x^2=16x^2+8x-48x^2+18x+3\)
\(\Leftrightarrow-32x^2=-32x^2+26x+3\)
\(\Leftrightarrow26x+3=0\)
\(\Leftrightarrow26x=-3\)
\(\Leftrightarrow x=-\dfrac{3}{26}\) (tmđk)
$Toru$