Giải các phương trình sau: z 4 -...

Khách

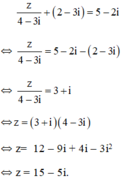
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

30 tháng 4 2017

Giải các phương trình sau: z 4 - 3 i + 2 - 3 i = 5 - 2 i

#Hỏi cộng đồng OLM #Toán lớp 12

Cao Minh Tâm

30 tháng 4 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Sách Giáo Khoa

1 tháng 4 2017

Giải các phương trình sau :

a) $\left(3-2i\right)z+\left(4+5i\right)=7+3i$

b) $\left(1+3i\right)z-\left(2+5i\right)=\left(2+i\right)z$

c) $\dfrac{z}{4-3i}+\left(2-3i\right)=5-2i$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Bảo Trung

1 tháng 4 2017

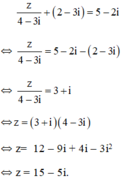
a) Ta có (3 - 2i)z + (4 + 5i) = 7 + 3i <=> (3 - 2i)z = 7 + 3i - 4 - 5i

<=> z = $\frac{3-2i}{3-2i}$ <=> z = 1. Vậy z = 1.

b) Ta có (1 + 3i)z - (2 + 5i) = (2 + i)z <=> (1 + 3i)z -(2 + i)z = (2 + 5i)

<=> (1 + 3i - 2 - i)z = 2 + 5i <=> (-1 + 2i)z = 2 + 5i

z = $\frac{2 + 5i}{-1+2i}=\frac{(2+5i)(-1-2i)}{5}=\frac{-2-4i-5i-10i^{2}}{5}=\frac{8-9i}{5}=\frac{8}{5}-\frac{9}{5}i$

Vậy z = $\frac{8}{5}-\frac{9}{5}i$

c) Ta có $\frac{z}{4-3i}$ + (2 - 3i) = 5 - 2i <=> $\frac{z}{4-3i}$ = 5 - 2i - 2 + 3i

<=> z = (3 + i)(4 - 3i) <=> z = 12 + 3 + (-9 + 4)i <=> z = 15 -5i

Đúng(0)

Sách Giáo Khoa

13 tháng 4 2017

Giải các phương trình sau trên tập số phức :

a) $3x^2+\left(2+2i\sqrt{2}\right)x-\dfrac{\left(1+i\right)^3}{1-i}=i\sqrt{8}x$

b) $\left(1-ix\right)^2+\left(3+2i\right)x-5=0$

#Hỏi cộng đồng OLM #Toán lớp 12

Sách Giáo Khoa

12 tháng 4 2017

Giải các phương trình sau trên tập số phức :

a) $\left(3+4i\right)x=\left(1+2i\right)\left(4+i\right)$

b) $2ix+3=5x+4i$

c) $3x\left(2-i\right)+1=2ix\left(1+i\right)+3i$

#Hỏi cộng đồng OLM #Toán lớp 12

Trần Minh Ngọc

26 tháng 3 2016

Giải phương trình

a) $z^3+8=0$

b) $z^6-z^3\left(1+i\right)+i=0$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Thái Bình

25 tháng 3 2016

$z^3+8=0$

$-8=8\left(\cos\pi+i\sin\pi\right)$

Các nghiệm là :

$z_k=2\left(\cos\frac{\pi+2k\pi}{3}+i\sin\frac{\pi+2k\pi}{3}\right);k=0,1,2$

b) $z^6-z^3\left(1+i\right)+i=0$

Phương trình tương đương với :

$\left(z^3-1\right)\left(z^3-i\right)=0$

Giải phương trình nhị thức $z^3-1=0,z^3-i=0$ có các nghiệm "

$\varepsilon=\cos\frac{2k\pi}{3}+\sin\frac{2k\pi}{3},k=0,1,2$

và :

$z_k=\cos\frac{\frac{\pi}{2}+2k\pi}{3}+i\sin\frac{\frac{\pi}{2}+2k\pi}{3},k=0,1,2$

Đúng(0)

Sách Giáo Khoa

12 tháng 4 2017

Giải phương trình sau trên tập số phức :

$\left(1-i\right)z+\left(2-i\right)=4-5i$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Thị Ty Nhung

16 tháng 5 2017

suy ra (1-i)z= (4-5i)-(2-i)

(1-i)z =2-4i

z= (2-4i)/(1-i)

z= 3-i

Đúng(0)

Tuyền Lê

5 tháng 10 2020

giải phương trình trên tập số phức:

3$x$+(2+3$i$)(1-2$i$)=5+4$i$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Việt Lâm

Giáo viên

5 tháng 10 2020

$\Leftrightarrow3x+8-i=5+4i$

$\Leftrightarrow3x=-3+5i$

$\Leftrightarrow x=-1+\frac{5}{3}i$

Đúng(0)

Sách Giáo Khoa

1 tháng 4 2017

Giải các phương trình sau trên tập số phức :

a) $\left(3+2i\right)z-\left(4+7i\right)=2-5i$

b) $\left(7-3i\right)z+\left(2+3i\right)=\left(5-4i\right)z$

c) $z^2-2z+13=0$

d) $z^4-z^2-6=0$

#Hỏi cộng đồng OLM #Toán lớp 12

Phan Thùy Linh

1 tháng 4 2017

a) (3 + 2i)z – (4 + 7i) = 2 – 5i

$\Leftrightarrow(3+2i)z=6+2i$

<=> z = $\dfrac{\text{6 + 2 i}}{\text{3 + 2 i}}$ = $\dfrac{22}{13}$ - $\dfrac{6}{13}$i

b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z

$\Leftrightarrow(7-3i-5+4i)=-2-3i$

⇔z= $\dfrac{\text{− 2 − 3 i}}{\text{2 + i}}$ = $\dfrac{-7}{5}$ - $\dfrac{4}{5}i$

c) z² – 2z + 13 = 0

⇔ (z – 1)² = -12 ⇔ z = 1 ± 2 √3 i

d) z⁴ – z²– 6 = 0

⇔ (z² – 3)(z² + 2) = 0

⇔ z ∈ { √3, - √3, √2i, - √2i}

Đúng(0)

CÔNG CHÚA THẤT LẠC

9 tháng 4 2017

Giải bài 15 trang 148 sgk Giải tích 12 | Để học tốt Toán 12

Đúng(0)

Sách Giáo Khoa

1 tháng 4 2017

Giải các phương trình sau trên tập số phức :

a) $\left(3+4i\right)z+\left(1-3i\right)=2+5i$

b) $\left(4+7i\right)z-\left(5-2i\right)=6iz$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Bảo Trung

1 tháng 4 2017

a) (3 + 4i)z = (2 + 5i) – (1 – 3i) = 1 + 8i

Vậy $z=1+8i3+4i=(1+8i)(3-4i)25=3525+2025i=75+45iz=1+8i3+4i=(1+8i)(3-4i)25=3525+2025i=75+45i$

b) (4 + 7i)z – (5 – 2i) = 6iz ⇔ (4 + 7i)z – 6iz = 5 – 2i

⇔ (4 + i)z = 5 – 2i

$\Leftrightarrowz=5-2i4+i=(5-2i)(4-i)17\Leftrightarrowz=1817-1317i$

Đúng(0)

Phạm Thái Dương

25 tháng 3 2016

Giải phương trình hệ số phức

$z^2-8\left(1-i\right)z+63-16i=0$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Hòa Bình

25 tháng 3 2016

$\Delta=\left(4-4i\right)^2-\left(63-16i\right)=-63-16i$

$r=\left|\Delta'\right|=\sqrt{63^2-16^2}=65$

Phương trình $y^2=-63-16i$

Có nghiệm $y_{1,2}=\pm\sqrt{\frac{65-63}{2}}+i\sqrt{\frac{65+63}{2}}=\pm\left(1-8i\right)$

Kéo theo

$z_{1,2}=4-4i\pm\left(1-8i\right)$

Do đó $z_1=5-12i,z_2=3+4i$

Ta cso thể dùng cách khác để giải phương trình bậc hai trên :

$\Delta'=\left(4-4i\right)^2-\left(63-16i\right)=-63-16i$

Tìm căn bậc hai của -63-16i, tức là tìm $z=x+yi,z^2=-63-16i$

$\Rightarrow x^2-y^2+2xyi=-63-16i$

$\Rightarrow\begin{cases}x^2-y^2=-63\\xy=-8\end{cases}$

$\Rightarrow\begin{cases}x=\pm1\\y=\pm8\end{cases}$

$\Delta'$

có 2 căn bậc 2 là $1-8i,-1+8i$

Phương trình có hai nghiệm

$z_1=4\left(1-i\right)+\left(1-8i\right)=5-12i$

$z_2=4\left(1-i\right)-\left(1-8i\right)=3+4i$

Đúng(0)

Sách Giáo Khoa

1 tháng 4 2017

Giải các phương trình sau trên tập hơn số phức :

a) $z^4+z^2-6=0$

b) $z^4+7z^2+10=0$

#Hỏi cộng đồng OLM #Toán lớp 12

Nguyễn Bảo Trung

1 tháng 4 2017

a) Đặt Z = z² , ta được phương trình Z² + Z – 6 = 0

Phương trình này có hai nghiệm là Z₁ = 2, Z₂ = -3

Vậy phương trình có bốn nghiệm là ± √2 và ± i√3.

b) Đặt Z = z² , ta được phương trình Z² + 7Z + 10 = 0

Phương trình này có hai nghiệm là Z₁ = -5, Z₂ = -2

Vậy phương trình có bốn nghiệm là ± i√2 và ± i√5.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP