Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a/
\(\Leftrightarrow sin2x\left(1+\sqrt{2}sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\1+\sqrt{2}sinx=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sinx=-\frac{\sqrt{2}}{2}=sin\left(-\frac{\pi}{4}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\x=-\frac{\pi}{4}+k2\pi\\x=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=-\frac{\pi}{4}+k2\pi\\x=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow2sin2x.cos2x-\frac{1}{2}sin4x+\frac{1}{2}sinx=0\)
\(\Leftrightarrow sin4x-\frac{1}{2}sin4x+\frac{1}{2}sinx=0\)
\(\Leftrightarrow sin4x=-sinx=sin\left(-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}4x=-x+k2\pi\\4x=\pi+x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{k2\pi}{5}\\x=\frac{\pi}{3}+\frac{k2\pi}{3}\end{matrix}\right.\)
e/
\(sin\left(\frac{3\pi}{2}-sinx\right)=1\)
\(\Leftrightarrow\frac{3\pi}{2}-sinx=\frac{\pi}{2}+k2\pi\)
\(\Leftrightarrow sinx=\pi+k2\pi\)
Mà \(-1\le sinx\le1\Rightarrow-1\le\pi+k2\pi\le1\)
\(\Rightarrow\) Không tồn tại k nguyên thỏa mãn
Pt đã cho vô nghiệm
f/
\(cos^2x-sin^2x+sin4x=0\)
\(\Leftrightarrow cos2x+2sin2x.cos2x=0\)
\(\Leftrightarrow cos2x\left(1+2sin2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin2x=-\frac{1}{2}=sin\left(-\frac{\pi}{6}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}+k\pi\\2x=-\frac{\pi}{6}+k2\pi\\2x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=-\frac{\pi}{12}+k\pi\\x=\frac{7\pi}{12}+k\pi\end{matrix}\right.\)

\(cos11x.cos3x=cos17x.cos9x\)
\(\Leftrightarrow\frac{1}{2}\left(cos24x+cos8x\right)=\frac{1}{2}\left(cos26x+cos8x\right)\)
\(\Leftrightarrow cos24x=cos26x\)
\(\Rightarrow\left[{}\begin{matrix}26x=24x+k2\pi\\26x=-24x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=\frac{k\pi}{25}\end{matrix}\right.\)
\(sin18x.cos13x=sin9x.cos4x\)
\(\Leftrightarrow\frac{1}{2}\left(sin31x+sin5x\right)=\frac{1}{2}\left(sin13x+sin5x\right)\)
\(\Leftrightarrow sin31x=sin13x\)
\(\Rightarrow\left[{}\begin{matrix}31x=13x+k2\pi\\31x=\pi-13x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{k\pi}{9}\\x=\frac{\pi}{44}+\frac{k\pi}{22}\end{matrix}\right.\)
\(sin2x-2sinx=0\)
\(\Leftrightarrow2sinx.cosx-2sinx=0\)
\(\Leftrightarrow sinx\left(cosx-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\cosx=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=k\pi\\x=k2\pi\end{matrix}\right.\) \(\Rightarrow x=k\pi\)
\(cosx.cos4x-cosx.cos2x=0\)
\(\Leftrightarrow cosx\left(cos4x-cos2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=0\\cos4x=cos2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\4x=2x+k2\pi\\4x=-2x+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=k\pi\\x=\frac{k\pi}{3}\end{matrix}\right.\)

Bài 7. a) sin 3x - cos 5x = 0 ⇔ cos 5x = sin 3x ⇔ cos 5x = cos (![]() - 3x) ⇔
- 3x) ⇔
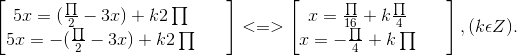
b) tan 3x . tan x = 1 ⇔ ![]() . Điều kiện : cos 3x . cos x # 0.
. Điều kiện : cos 3x . cos x # 0.
Với điều kiện này phương trình tương đương với
cos 3x . cos x = sin 3x . sinx ⇔ cos 3x . cos x - sin 3x . sinx = 0 ⇔ cos 4x = 0.
Do đó
tan 3x . tan x = 1 ⇔ ![]()
![]()
⇔ cos 2x = ![]() ⇔ cos 4x = 0
⇔ cos 4x = 0
⇔ ![]()


a) Đặt t = cosx, t ∈ [-1 ; 1] ta được phương trình 2t2 - 3t + 1 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Nghiệm của phương trình đã cho là các nghiệm của hai phương trình sau:
cosx = 1 ⇔ x = k2π và cosx = ![]() ⇔ x =
⇔ x = ![]() + k2π.
+ k2π.
Đáp số : x = k2π ; x = ![]() + k2π, k ∈ Z.
+ k2π, k ∈ Z.
b) Ta có sin4x = 2sin2xcos2x (công thức nhân đôi), do đó phương trình đã cho tương đương với
2sin2x(1 + √2cos2x) = 0 ⇔ ![]()
⇔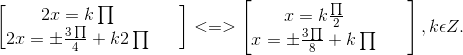

cosx.cos2x = 1 + sinx.sin2x
⇔ cosx.cos2x - sinx.sin2x = 1
⇔ cos3x = 1 ⇔ 3x = k2π