Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
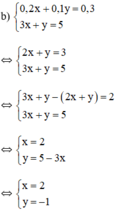
Vậy hệ phương trình có nghiệm duy nhất (2; -1).
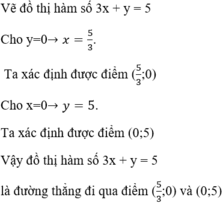
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
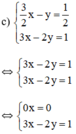
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng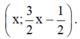 
KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm
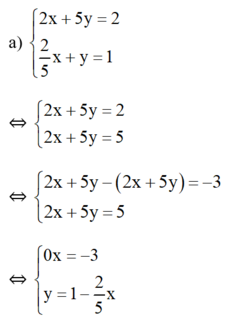
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
Minh họa hình học:
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng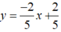 
(d1)
Tập nghiệm của phương trình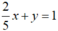 
được biểu diễn bởi đường thẳng 
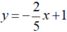(d2).
KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm
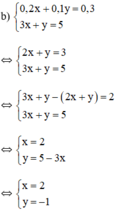
Vậy hệ phương trình có nghiệm duy nhất (2; -1).
KL: Đồ thị hai hàm số trên cắt nhau tại điểm (2; -1). Vậy (2; -1) là nghiệm của hệ phương trình
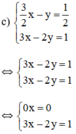
Phương trình 0x = 0 nghiệm đúng với mọi x nên hệ phương trình có vô số nghiệm dạng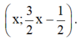 
KL: Đồ thị hai hàm số trên trùng nhau. Vậy hệ phương trình có vô số nghiệm
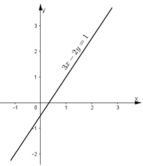
a) Giải hệ phương trình:
{2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′){2x+5y=2(1)25x+y=1(2)⇔{2x+5y=2(1′)−2x−5y=−5(2′)
Cộng (1’) với (2’) vế theo vế, ta được: 0x + 0y = -3
Phương trình này vô nghiệm. Vậy hệ đã cho vô nghiệm.
Minh họa hình học kết quả tìm được:
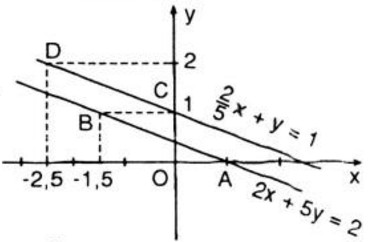
- Vẽ đồ thị hàm số 2x + 5y = 2.
Cho y = 0 ⇒ x = 1. Ta xác định được điểm A(1; 0)
Cho y = 1 ⇒ x = -1,5. Ta xác định được điểm B(-1,5; 1).
Đồ thị hàm số là đường thẳng đi qua hai điểm A và B
-Vẽ đồ thị hàm số 25x+y=1⇔2x+5y=525x+y=1⇔2x+5y=5
Cho x = 0 ⇒ y = 1. Ta xác định được điểm C(0; 1)
Cho y = 2 ⇒ x = -2,5. Ta xác định được điểm D(-2,5; 2)
Đồ thị hàm số là đường thẳng đi qua hai điểm C và D.
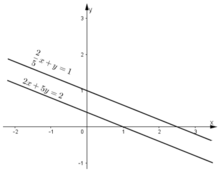
Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.
b) Giải hệ phương trình:
{0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′){0,2x+0,1y=0,3(1)3x+y=5(2)⇔{−2x−y=−3(1′)3x+y=5(2′)
Cộng (1’) với (2’) vế theo vế, ta được x = 2
Thế x = 2 vào (2), ta được: 6 + y = 5 ⇔ y = -1
Vậy nghiệm của hệ phương trình là (x = 2; y = -1)
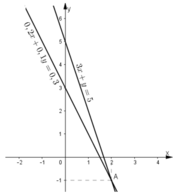
Minh họa hình học:
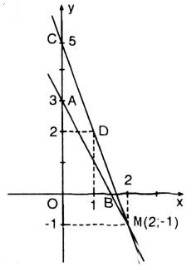
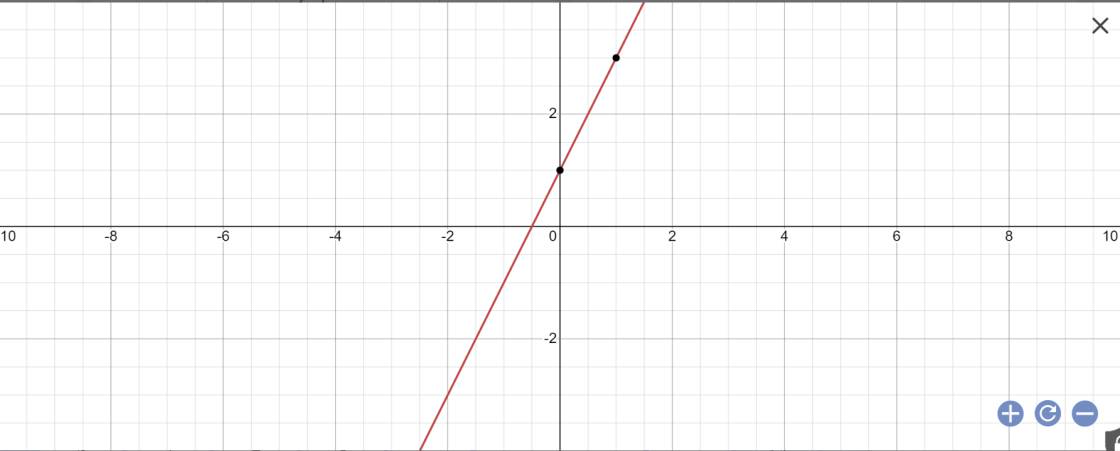
- Đồ thị hàm số 0,2x + 0,1y = 0,3 là một đường thẳng đi qua hai điểm:
A(x = 0; y = 3) và B(x = 1,5; y = 0)
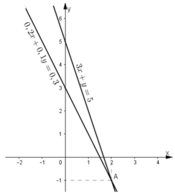
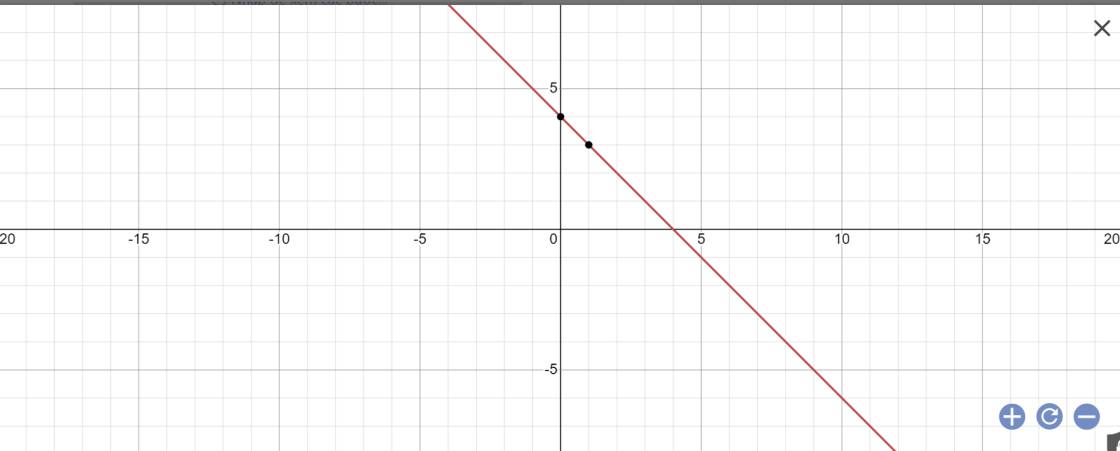
- Đồ thị hàm số 3x + y = 5 là một đường thẳng đi qua hai điểm C(x = 0; y = 5) và D(x = 1; y = 2)
- Đồ thị hai hàm số trên cắt nhau tại điểm: M(x = 2; y = -1).
Vậy (2; -1) là một nghiệm của hệ phương trình.
c) Giải hệ phương trình:
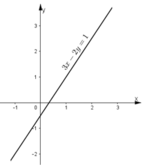
{32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′){32x−y=12(1)3x−2y=1(2)⇔{−3x+2y=−1(1′)3x−2y=1(2′)
Cộng (1’) và (2’) vế theo vế, ta có: 0x + 0y = 0.
Phương trình này có vô số nghiệm.
Nghiệm tổng quát là (x;32x−12)(x;32x−12) với x ∈ R
Minh họa hình học
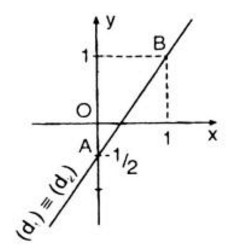
- Đồ thị hàm số (1) là đường thẳng đi qua hai điểm A(0; −12−12) và B(1;1) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.
a)
5x2−3x=0⇔x(5x−3)=05x2−3x=0⇔x(5x−3)=0
⇔ x = 0 hoặc 5x – 3 =0
⇔ x = 0 hoặc x=35.x=35. Vậy phương trình có hai nghiệm: x1=0;x2=35x1=0;x2=35
Δ=(−3)2−4.5.0=9>0√Δ=√9=3x1=3+32.5=610=35x2=3−32.5=010=0Δ=(−3)2−4.5.0=9>0Δ=9=3x1=3+32.5=610=35x2=3−32.5=010=0
b)
3√5x2+6x=0⇔3x(√5x+2)=035x2+6x=0⇔3x(5x+2)=0
⇔ x = 0 hoặc √5x+2=05x+2=0
⇔ x = 0 hoặc x=−2√55x=−255
Vậy phương trình có hai nghiệm: x1=0;x2=−2√55x1=0;x2=−255
Δ=62−4.3√5.0=36>0√Δ=√36=6x1=−6+62.3√5=06√5=0x2=−6−62.3√5=−126√5=−2√55Δ=62−4.35.0=36>0Δ=36=6x1=−6+62.35=065=0x2=−6−62.35=−1265=−255
c)
2x2+7x=0⇔x(2x+7)=02x2+7x=0⇔x(2x+7)=0
⇔ x = 0 hoặc 2x + 7 = 0
⇔ x = 0 hoặc x=−72x=−72
Vậy phương trình có hai nghiệm: x1=0;x2=−72x1=0;x2=−72
Δ=72−4.2.0=49>0√Δ=√49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72Δ=72−4.2.0=49>0Δ=49=7x1=−7+72.2=04=0x2=−7−72.2=−144=−72
d)
2x2−√2x=0⇔x(2x−√2)=02x2−2x=0⇔x(2x−2)=0
⇔ x = 0 hoặc 2x−√2=02x−2=0
⇔ x = 0 hoặc x=√22x=22
Δ=(−√2)2−4.2.0=2>0√Δ=√2x1=√2+√22.2=2√24=√22x2=√2−√22.2=04=0
c) Có \(P=\frac{ax+b}{x^2+1}=-1+\frac{x^2+ax+b+1}{x^2+1}\);
\(P=\frac{ax+b}{x^2+1}=4-\frac{4x^2-ax-b+4}{x^2+1}\)
Để Min P = 1 và Max P = 4 thì
\(\hept{\begin{cases}x^2+ax+b+1=\left(x+c\right)^2\\4x^2-ax-b+4=\left(2x+d\right)^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\left(a-2c\right)+\left(b+1-c^2\right)=0\left(1\right)\\x\left(-a-4d\right)+\left(-b+4-d^2\right)=0\left(2\right)\end{cases}}\)
(1) = 0 khi \(\hept{\begin{cases}a=2c\\b=c^2-1\end{cases}}\)(3)
(2) = 0 khi \(\hept{\begin{cases}a=-4d\\b=4-d^2\end{cases}}\)(4)
Từ (3) (4) => d = 1 ; c = -2 ; b = 3 ; a = -4
Vậy \(P=\frac{-4x+3}{x^2+1}\)
ĐK \(x\ge y\)
Đặt \(\sqrt{x+y}=a;\sqrt{x-y}=b\left(a;b\ge0\right)\)
HPT <=> \(\hept{\begin{cases}a^4+b^4=82\\a-2b=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(2b+1\right)^4+b^4=82\\a=2b+1\end{cases}}\Leftrightarrow\hept{\begin{cases}17b^4+32b^3+24b^2+8b-81=0\\a=2b+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}17b^4-17b^3+49^3-49b^2+73b^2-73b+81b-81=0\\a=2b+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(b-1\right)\left(17b^3+49b^2+73b+81\right)=0\left(1\right)\\a=2b+1\end{cases}}\)
Giải (1) ; kết hợp điều kiện => b = 1
=> Hệ lúc đó trở thành \(\hept{\begin{cases}b=1\\a=2b+1\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\a=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x+y}=3\\\sqrt{x-y}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=9\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}2x=10\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\\y=4\end{cases}}\)
Vậy hệ có 1 nghiệm duy nhất (x;y) = (5;4)
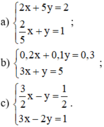
Phương trình 0x = -3 vô nghiệm nên hệ phương trình vô nghiệm.
Minh họa hình học:
Tập nghiệm của phương trình 2x + 5y = 2 được biểu diễn bởi đường thẳng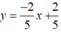
(d1)
Tập nghiệm của phương trình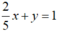
được biểu diễn bởi đường thẳng 
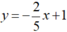(d2).
KL: Đồ thị hai hàm số trên song song. Điều này chứng tỏ hệ phương trình trên vô nghiệm