Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: =>4x+12<=2x-1
=>2x<=-13
=>x<=-13/2
b: =>x^2-2x+1+4<0
=>(x-1)^2+4<0(loại)
c: =>(x-2+x+3)/(x+3)<0
=>(2x+1)/(x+3)<0
=>-3<x<-1/2

a) \(4x^2-x+1< 0\)
Tam thức f(x) = 4x2 - x + 1 có hệ số a = 4 > 0 biệt thức ∆ = 12 – 4.4 < 0. Do đó f(x) > 0 ∀x ∈ R.
Bất phương trình 4x2 - x + 1 < 0 vô nghiệm.
b) f(x) = - 3x2 + x + 4 = 0
\(\Delta=1^2-4\left(-3\right).4=49\)
\(x_1=\dfrac{-1+\sqrt{49}}{-3}=-1\)
\(x_2=\dfrac{-1-\sqrt{49}}{-3.2}=\dfrac{4}{3}\)
- 3x2 + x + 4 ≥ 0 <=> - 1 ≤ x ≤ .

từ câu 1 đến câu 4 bạn có thẻ dùng máy tính casio f(x)570 VN giải nhé .bạn bấm MODE xuống 1 1
1)vô nghiệm
2)vô nghiệm
3)luôn đúng
4)\(\frac{-1-\sqrt{41}}{4}\le x\le\frac{-1+\sqrt{41}}{4}\)
5) \(\left\{{}\begin{matrix}-2x^2+5x-2\le x-3\\-2x^2+5x-2\ge-x+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le\frac{2-\sqrt{6}}{2}\\x\ge\frac{2+\sqrt{6}}{2}\end{matrix}\right.\\vonghiem\end{matrix}\right.\) vậy bpt vô nghiệm

Câu 6:
\(\hept{\begin{cases}\frac{x+3}{2x-3}-\frac{x}{2x-1}\le0\\\sqrt{x^2+3}+3< 1\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2x^2-x+6x-3-2x^2+3x}{\left(2x-3\right)\left(2x-1\right)}\le0\\x^2+3< \left(1-3x\right)^2\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}8x-3\le0\\x^2+3< 1-6x+9x^2\end{cases}\Leftrightarrow\hept{\begin{cases}8x-3\le0\\8x^2-6x-2< 0\end{cases}\Leftrightarrow}\hept{\begin{cases}x< \frac{3}{8}\\\frac{-1}{4}x< x< \frac{1}{4}\end{cases}\Rightarrow}S\left(\frac{-1}{4};\frac{3}{8}\right)}\)

\(21,\frac{2}{x-1}\le\frac{5}{2x-1}\left(x\ne1;x\ne\frac{1}{2}\right)\)
\(\Leftrightarrow\frac{2}{x-1}-\frac{5}{2x-1}\le0\)
\(\Leftrightarrow\frac{4x-2-5x+5}{\left(x-1\right)\left(2x-1\right)}\text{≤}0\)
\(\Leftrightarrow\frac{-x+3}{\left(x-1\right)\left(2x-1\right)}\text{≤}0\)
x -x+3 x-1 2x-1 VT -∞ +∞ 1/2 1 3 0 0 0 | | || | | || | | 0 - + + + + + - - - + + + + + + - -
Vậy \(\frac{-x+3}{\left(x-1\right)\left(2x-1\right)}\le0\Leftrightarrow x\in\left(\frac{1}{2};1\right)\cup[3;+\text{∞})\)
23,24 tương tự 21
\(25,2x^2-5x+2< 0\) (1)
Ta có: \(\left\{{}\begin{matrix}2x^2-5x+2=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\frac{1}{2}\end{matrix}\right.\\a=2>0\end{matrix}\right.\) \(\Leftrightarrow\frac{1}{2}< x< 2\)
\(26,-5x^2+4x+12< 0\)
\(\left\{{}\begin{matrix}-5x^2+4x+12=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\frac{6}{5}\end{matrix}\right.\\a=-5< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\x< -\frac{6}{5}\end{matrix}\right.\)
\(27,16x^2+40x+25>0\)
\(\left\{{}\begin{matrix}16x^2+40x+25=0\Leftrightarrow x=-\frac{5}{4}\\a=16>0\end{matrix}\right.\)
\(\Leftrightarrow x\ne-\frac{5}{4}\)
\(28,-2x^2+3x-7\ge0\)
\(\left\{{}\begin{matrix}-2x^2+3x-7=0\left(vo.nghiem\right)\\a=-2< 0\end{matrix}\right.\)
\(\Rightarrow-2x^2+3x-7< 0\) ∀x
=> bpt vô nghiệm
\(29,3x^2-4x+4\ge0\)
\(\left\{{}\begin{matrix}3x^2-4x+4=0\left(vo.nghiem\right)\\a=3>0\end{matrix}\right.\)
=> \(3x^2-4x+4>0\) => bpt vô số nghiệm
\(30,x^2-x-6\le0\)
\(\left\{{}\begin{matrix}x^2-x-6=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\\a=1>0\end{matrix}\right.\)
\(\Rightarrow-2\le x\le3\)

a/ \(\Leftrightarrow\left(4-x\right)\left(x+1\right)\left(x-8\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}x< -1\\4< x< 8\end{matrix}\right.\)
b/ \(\frac{1-2x}{x}\le0\Rightarrow\left[{}\begin{matrix}x\ge\frac{1}{2}\\x< 0\end{matrix}\right.\)
c/ \(\left|2x+1\right|< 3x\)
- Với \(x< 0\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT vô nghiệm
- Với \(x>0\Rightarrow2x+1>0\)
\(BPT\Leftrightarrow2x+1< 3x\Rightarrow x>1\)
d/ \(\sqrt{3x+1}\le x+1\)
ĐKXĐ: \(x\ge-\frac{1}{3}\)
DO 2 vế của BPT ko âm, bình phương 2 vế:
\(\left(x+1\right)^2\ge3x+1\)
\(\Leftrightarrow x^2-x\ge0\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le0\end{matrix}\right.\)
Kết hợp ĐKXĐ \(\Rightarrow\left[{}\begin{matrix}-\frac{1}{3}\le x\le0̸\\x\ge1\end{matrix}\right.\)
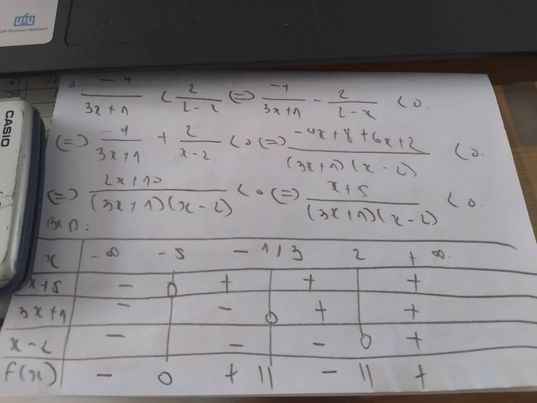

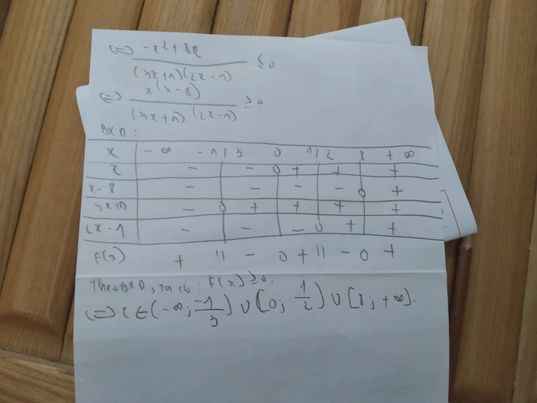
a: =>(x-1)(x-2)<=0
=>1<=x<=2
b: =>(x^2-1)(x^2-2)<=0
=>1<=x^2<=2
=>\(\left[{}\begin{matrix}1< =x< =\sqrt{2}\\-1>=x>=-\sqrt{2}\end{matrix}\right.\)