
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Ta có A = sin4x + cos4x - ¼cos 4x = ( sin2x + cos2x) 2 - 2sin2x.cos2x - ¼cos 4x
= 1 - ½sin22x - ¼cos4x = 1 - ¼(1 – cos4x) - ¼cos4x = 3/4

Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.

Chọn C.
Ta có: C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
= 2 [ (sin2x + cos2x) 2 - sin2x.cos2x]2 - [ (sin4x + cos4x)2 - 2sin4x.cos4x]
= 2[ 1 - sin2x.cos2x]2 - [ (sin2x+ cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1- sin2x.cos2x]2 - [ 1 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2xcos2x+ sin4x.cos4x) –( 1- 4sin2xcos2x+ 4sin4xcos4x) + 2sin4x.cos4x
= 1.

\(\frac{sin2x-sin4x}{1-cos2x+cos4x}=\frac{sin2x-2sin2x.cos2x}{1-cos2x+2cos^22x-1}=\frac{sin2x\left(1-2cos2x\right)}{-cos2x\left(1-2cos2x\right)}=\frac{-sin2x}{cos2x}=-tan2x\)
\(\frac{sin4x-sin2x}{1-cos2x+cos4x}=-\left(\frac{sin2x-sin4x}{1-cos2x+cos4x}\right)=-\left(-tan2x\right)=tan2x\) lấy luôn kết quả câu trên cho lẹ, biến đổi thì làm y hệt

\(\frac{sin4x-sin2x}{1-cos2x+cos4x}=\frac{2sin2x.cos2x-sin2x}{1-cos2x+2cos^22x-1}=\frac{sin2x\left(2cos2x-1\right)}{cos2x\left(2cos2x-1\right)}=\frac{sin2x}{cos2x}=tan2x\)
\(\Rightarrow\) đề sai
b/
\(\frac{1-cos4x}{sin4x}=\frac{1-\left(1-2sin^22x\right)}{2sin2x.cos2x}=\frac{2sin^22x}{2sin2x.cos2x}=\frac{sin2x}{cos2x}=tan2x\)
Đề sai tiếp lần 2

\(A=\frac{1}{2}\left(\frac{sin^2x}{cos^2x}-1\right)\frac{cosx}{sinx}+cos4x.cot2x+sin4x\)
\(A=\frac{-1}{2}\left(\frac{cos^2x-sin^2x}{cos^2x}\right)\frac{cosx}{sinx}+cos4x.cot2x+sin4x\)
\(A=\frac{-cos2x}{2cosx.sinx}+cos4x.cot2x+sin4x\)
\(A=-cot2x+cos4x.cot2x+sin4x\)
\(A=cot2x\left(cos4x-1\right)+sin4x\)
\(A=\frac{cos2x}{sin2x}.\left(1-2sin^22x-1\right)+sin4x\)
\(A=\frac{-2cos2x.sin^22x}{sin2x}+sin4x\)
\(A=-sin4x+sin4x=0\)

a) \(sin^4x+cos^4x=\left(sin^2x\right)^2+\left(cos^2x\right)^2\)
\(=\left(sin^2x\right)^2+2sin^2xcos^2x+\left(cos^2x\right)^2-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\)
b) \(\dfrac{1+cotx}{1-cotx}=\dfrac{tanx.cotx+cotx}{tanx.cotx-cotx}\)
\(=\dfrac{cotx.\left(tanx+1\right)}{cotx.\left(tanx-1\right)}\)
\(=\dfrac{tanx+1}{tanx-1}\)
c) \(\dfrac{cosx+sinx}{cos^3x}=\dfrac{1}{cos^2x}+\dfrac{tanx}{cos^2x}\)
\(=1+tan^2x+tanx.\dfrac{1}{cos^2x}\)
\(=1+tan^2x+tanx.\left(1+tan^2x\right)\)
\(=1+tan^2x+tanx+tan^3x\)
\(=tan^3x+tan^2x+tanx+1\)

Lời giải:
a.
$\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-2\sin ^2x\cos ^2x$
b.
$\frac{1+\cot x}{1-\cot x}=\frac{1+\frac{\cos x}{\sin x}}{1-\frac{\cos x}{\sin x}}=\frac{\cos x+\sin x}{\sin x-\cos x}(1)$
$\frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}+1}{\frac{\sin x}{\cos x}-1}=\frac{\cos x+\sin x}{\sin x-\cos x}(2)$
Từ $(1); (2)$ ta có đpcm
c.
$\frac{\cos x+\sin x}{\cos ^3x}=(1+\frac{\sin x}{\cos x}).\frac{1}{\cos ^2x}$
$=(1+\tan x).\frac{\sin ^2x+\cos ^2x}{\cos ^2x}$
$=(1+\tan x)(\tan ^2x+1)=\tan ^3x+\tan ^2x+\tan x+1$
Ta có đpcm.
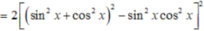

 không phụ thuộc vào x.
không phụ thuộc vào x.

