Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HÌnh bạn tự vẽ.
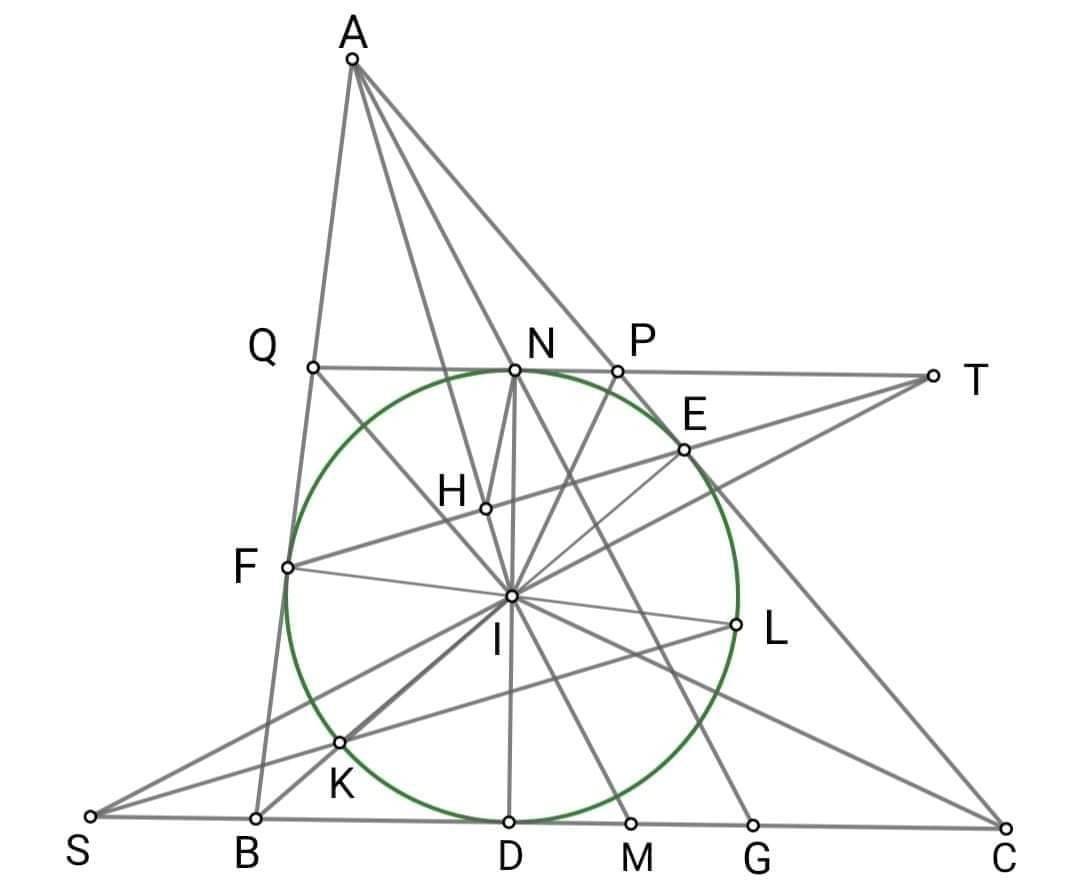
Bổ đề: (định lý Ptô-lê-mê)
Trong một tứ giác nội tiếp ABCD, ta có:
AC . BD = AB . CD + BC . AD
Áp dụng bổ đề trên cho tứ giác nội tiếp IPAN, ta có IA.NP = IP.AN + IN.AP = 2r(p - a) (ở đây ta đặt BC = a, CA = b, AB = c) và
\(p=\frac{a+b+c}{2}\) thì AN = AP = p - a.
Tương tự IB . PM = 2r(p - b)
IC . MN = 2r(p - c)
Nhân theo vế ba đẳng thức trên ta được:
\(IA.IB.IC.MN.NP.PM=8r^3\left(p-a\right)\left(p-b\right)\left(p-c\right)\).
Mặt khác, vì r là bán kính đường tròn ngoại tiếp \(\Delta MNP\)nên MN.NP.PM = \(4rS_{MNP}\).
Ngoài ra theo công thức Hê-rông ta có:
\(S_{ABC}=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\).Do đó:
IA . IB . IC. 4rSMNP = \(\frac{8r^3.S^2_{ABC}}{p}=8r^4S_{ABC}\)(vì SABC = pr), suy ra đpcm
P/s: Chỗ nào không hiểu thì bạn chỉ việc vẽ hình ra và quan sát hình là được :))

Trả lời:
a) Xét tam giác AHI và AKI có :
AI là cạnh chung
góc HAI =góc KAI
góc H = góc K (=90)
suy ra tam giác AHI = tam giác AKI (cạnh huyền - góc nhọn )
suy ra góc AIH =AIK (hai góc tg ứng)
suy ra góc HIB = KIC (cùng kề vs hai góc bằng nhau )
xét tam giác HIB và KIC có
HIB = KIC (chứng minh trên )
BHI=CKI (=90)
BI=IC
suy ra tam giác HIB=KIC(cạnh huyền góc nhọn )
suy ra BH=CK ( hai cạnh tương ứng ) (điều phải chứng minh )
b) Xét tam giác AHI và AKI có :
AI là cạnh chung
góc HAI =góc KAI
góc H = góc K (=90)
suy ra tam giác AHI = tam giác AKI (cạnh huyền - góc nhọn )
suy ra góc AIH =AIK (hai góc tg ứng)
suy ra góc HIB = KIC (cùng kề vs hai góc bằng nhau )
xét tam giác HIB và KIC có
HIB = KIC (chứng minh trên )
BHI=CKI (=90)
BI=IC
suy ra tam giác HIB=KIC(cạnh huyền góc nhọn )
suy ra BH=CK ( hai cạnh tương ứng ) (đpcm)
~Học tốt!~

a, Xét tg AHI và tg AKI ta có:
góc H = góc K = 90
AI là cạnh chung
góc HAI = góc KAI ( AI là tia phân giác góc BAC)
=> tg AHI =tg AKI ( cạnh huyền-góc nhọn)
=> AH=AK

A B C D a)
ta có D là giao điểm của cung tròn tâm B với cung tròn tâm C=>BD là bán kính của cung tròn tâm B và CD là bán kính của cung tròn tâm C
ta có: DB là bán kính của cung tròn tâm B mà AC cũng là bán kính của cung tròn tâm B=> AC=BD
CM tương tự ta có: CD=AB
xét \(\Delta ABC\) và \(\Delta DCB\) có:
BD=AC(cmt)
AB=DC(cmt)
BC(chung)
\(\Rightarrow\Delta ABC=\Delta DCB\left(c.c.c\right)\)
=>\(\widehat{BAC}=\widehat{BDC}=80^o\)
b)
theo câu a, ta có:
\(\Delta ABC=\Delta DCB\Rightarrow\widehat{ABC}=\widehat{BCD}\)
=>CD//AB(2 góc slt)
A B C D Nếu bạn xem ko đc hình thì xem hình này cũng được, khi nãy mk vẽ quên căn
ở câu a, mk ko quen cách diễn đạt lớp 9 cho lắm nên thông cảm nhé

Bài 7 :
( bạn đạt A = (...) cái biểu thức đấy nhé, tự đặt )
Ta có :
\(\frac{1}{\sqrt{1}}=\frac{1}{1}>\frac{1}{10}=\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{100}}\)
\(............\)
\(\frac{1}{\sqrt{100}}=\frac{1}{\sqrt{100}}\)
\(\Rightarrow\)\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}>\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\)
\(A>\frac{100}{\sqrt{100}}=\frac{100}{10}=10\)
\(\Rightarrow\)\(A>10\)
Vậy \(A>10\)
Chúc bạn học tốt ~
Bạn làm được mình bài 7 thôi à, mình thấy bạn giỏi lắm mà. Mình có tới mấy chục bài cần giải cơ. Dạo này mình hỏi nhiều vì sắp đi thi.