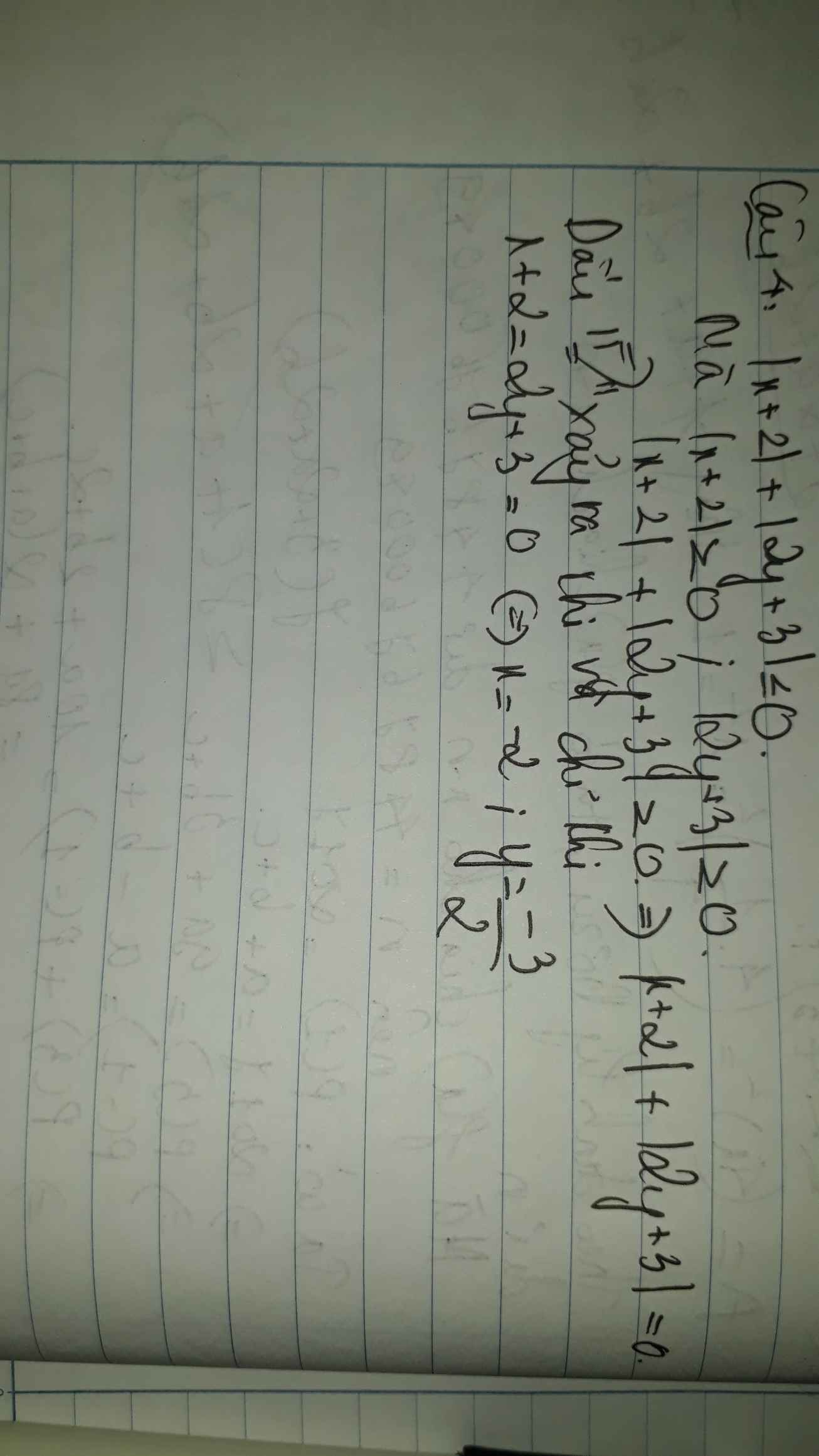VT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
1
PN
10
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
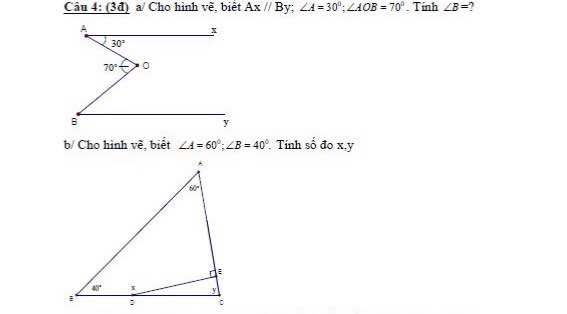
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
6 tháng 9 2021
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
5 tháng 1 2020
hình em tự vẽ nhé
Xét tam giác AND có H là trung điểm của AN,M là trung điểm của AD(gt)
\(\Rightarrow HM\)là đường trung bình của tam giác AND
\(\Rightarrow HM//ND\)
Mà \(H\in BC;M\in BC\)
\(\Rightarrow BC//ND\)
NT
2
28 tháng 8 2021
Câu 4:
Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|2y+3\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|2y+3\right|\ge0\forall x,y\)
Dấu '='xảy ra khi x=-2 và \(y=-\dfrac{3}{2}\)
14 tháng 4 2020
ai giải bải này cko mik với ạ mik cảm ơn
một thửa ruộng hình chữ nhật có chiều dài 54m, chiếu rộng bằng 2/3 chiều dài người ta cấy lúa trên thửa ruộng đó trung bình 100m vuông thu được 70kg thóc .Hỏi cả thửa ruộng thu được bao nhiêu tạ thóc
14 tháng 4 2020
A B C H
a) Vì \(\Delta ABC\)là tam giác cân tại A
=> \(AB=AC\)và \(\widehat{B}=\widehat{C}\)
CM \(\Delta AHB=\Delta AHC\)
Xét \(\Delta AHB\)và \(\Delta AHC\)có :
\(AB=AC\left(cmt\right)\)
\(\widehat{B}=\widehat{C}\left(cmt\right)\)
\(HB=HC\)( vì M là trung điểm của BC )
=> \(\Delta AHB=\Delta AHC\left(c.g.c\right)\)
b) CM \(AH\perp BC\)
Vì \(\Delta AHB=\Delta AHC\)
=> \(\widehat{H_1}=\widehat{H_2}\)( hai góc tương ứng ) ( chỗ này mình vẽ thiếu, bạn tự bổ sung )
mà \(\widehat{H_1}+\widehat{H_2}=180^0\)( kề bù )
=> \(\widehat{H}_1=\widehat{H_2}=\frac{180^0}{2}=90^0\)
=> \(AH\perp BC\)( đpcm )
d) Nếu AB = 5cm , AH = 3cm . Tính BC
Vì \(\widehat{H_1}=90^0\)=> \(\Delta AHB\)là tam giác vuông
=> \(AB^2=AH^2+BC^2\)( Đ/lí Pytago )
Thay AB = 5cm, AH = 3cm ta có
\(5^2=3^2+BC^2\)
\(25=9+BC^2\)
=> \(BC^2=16\)
mà \(\sqrt{16}=4\)=> BC = 4cm