Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi m = 0 phương trình trở thành 4 x 2 = 4 nhận x = 1 và x = -1 là nghiệm. Vì thay x = 1 và x = -1 thì VT = VP = 4.

\(\left(x+4\right)\left(9x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\9x^2-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x^2=\dfrac{1}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\pm\dfrac{1}{3}\end{matrix}\right.\)\(S=\left\{-4,\pm\dfrac{1}{3}\right\}\)
Ta có: \(\left(x+4\right)\left(9x^2-1\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\3x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\3x=1\\3x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy: \(S=\left\{-4;\dfrac{1}{3};-\dfrac{1}{3}\right\}\)

1) \(x^4-6x^3-x^2+54x-72=0\)
\(\Leftrightarrow x^3\left(x-2\right)-4x^2\left(x-2\right)-9x\left(x-2\right)+36\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3-4x^2-9x+36\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x-4\right)-9\left(x-4\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)\left(x^2-9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)\left(x-3\right)\left(x+3\right)=0\)
Tự làm nốt...
2) \(x^4-5x^2+4=0\)
\(\Leftrightarrow x^2\left(x^2-1\right)-4\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)=0\)
Tự làm nốt...
\(x^4-2x^3-6x^2+8x+8=0\)
\(\Leftrightarrow x^3\left(x-2\right)-6x\left(x-2\right)-4\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3-6x-4\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+2\right)-2x\left(x+2\right)-2\left(x+2\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left[\left(x-1\right)^2-\left(\sqrt{3}\right)^2\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)\left(x-1-\sqrt{3}\right)\left(x-1+\sqrt{3}\right)=0\)
...
\(2x^4-13x^3+20x^2-3x-2=0\)
\(\Leftrightarrow2x^3\left(x-2\right)-9x^2\left(x-2\right)+2x\left(x-2\right)+\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^3-9x^2+2x+1\right)=0\)
Bí

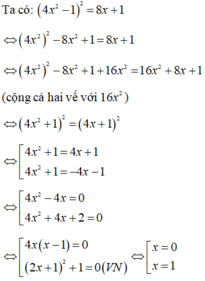
Tập nghiệm của phương trình là S = {0; 1}
Suy ra nghiệm lớn nhất của phương trình là x 0 = 1 < 2
Đáp án cần chọn là B
PT\(\Leftrightarrow-5x^2+6x-1=0\)
\(\Leftrightarrow5x^2-6x+1=0\)
=>5x2-5x-x+1=0
=>(x-1)(5x-1)=0
=>x=1 hoặc x=1/5